Ray-Plane and Ray-Disk Intersection
Reading time: 4 mins.Ray-Plane Intersection
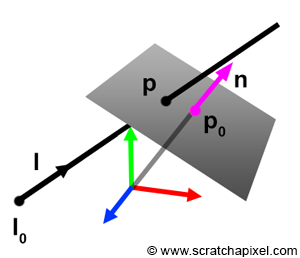
In this chapter, we explore how to calculate the intersection of a ray with a plane and a disk. From our Geometry lesson, we know that the dot (or scalar) product of two vectors perpendicular to each other always equals 0:
$$A \cdot B = 0$$This holds true specifically when vectors \(A\) and \(B\) are perpendicular. A plane is characterized by a point \(p_0\), indicating its distance from the world's origin, and a normal \(n\), which defines the plane's orientation. We can derive a vector on the plane from any point \(p\) on it by subtracting \(p_0\) from \(p\). Since this resultant vector lies within the plane, it is perpendicular to the plane's normal. Leveraging the property that the dot product of two perpendicular vectors equals 0, we have (equation 1):
$$(p - p_0) \cdot n = 0$$Likewise, a ray is described using the parametric form (equation 2):
$$l_0 + l * t = p$$Here, \(l_0\) represents the ray's origin, and \(l\) denotes the ray's direction. This implies we can pinpoint any position along the ray using the ray's origin, its direction, and the scalar \(t\), a positive real number signifying the parametric distance from the ray's origin to the point of interest. If the ray intersects the plane, they share a point \(p\) at the intersection. Substituting equation 2 into equation 1 gives us:
$$(l_0 + l * t - p_0) \cdot n = 0 $$Our goal is to find a value for \(t\) that allows us to compute the intersection point's position using the ray's parametric equation. Solving for \(t\), we obtain:
$$ t = -{\dfrac{(l_0-p_0)\cdot n}{l \cdot n}} = {\dfrac{(p_0 - l_0) \cdot n}{l \cdot n}} $$It's worth noting that if the plane and ray are parallel (i.e., when \(l \cdot n\) approaches 0), they either perfectly coincide, offering an infinite number of solutions, or they do not intersect at all. In practical C++ implementations, we typically return false (indicating no intersection) when the denominator is less than a very small threshold.
bool intersectPlane(const Vec3f &n, const Vec3f &p0, const Vec3f &l0, const Vec3f &l, float &t)
{
// Assuming vectors are all normalized
float denom = dotProduct(n, l);
if (denom > 1e-6) {
Vec3f p0l0 = p0 - l0;
t = dotProduct(p0l0, n) / denom;
return (t >= 0);
}
return false;
}
Ray-Disk Intersection
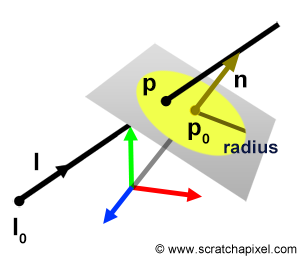
The procedure for determining a ray-disk intersection is straightforward. Typically, a disk is defined by its position (the center of the disk), a normal, and a radius. The initial step involves checking if the ray intersects the plane where the disk resides. For this ray-plane intersection phase, we can employ the code developed for the ray-plane intersection test. If there's an intersection with the plane, the next step is to calculate the intersection point and measure the distance from this point to the disk's center. The ray intersects the disk if this distance is less than or equal to the disk's radius. As an optimization, instead of directly calculating the distance, you can compare the square of the distance against the square of the disk's radius. This squared distance can be derived from the dot product of vector \(v\) (in the code) with itself. Computing the actual distance would necessitate taking the square root of this dot product. However, for efficiency, we can compare the dot product result directly against the square of the radius (often precalculated), thereby avoiding the costly square root operation.
bool intersectDisk(const Vec3f &n, const Vec3f &p0, const float &radius, const Vec3f &l0, const Vec3f &l)
{
float t = 0;
if (intersectPlane(n, p0, l0, l, t)) {
Vec3f p = l0 + l * t; // Calculate intersection point
Vec3f v = p - p0; // Vector from disk center to intersection point
float d2 = dotProduct(v, v); // Squared distance from disk center to intersection point
// return (sqrtf(d2) <= radius); // Direct distance comparison (less efficient)
// The optimized method (using precomputed radius squared):
return d2 <= radius * radius; // Compare squared distances (more efficient)
}
return false;
}