A Creative Dive into BRDF, Linearity, and Exposure

An Introduction for Artists to BRDFs and Radiometry

Reading time: 15 mins.

This lesson was originally written in the early 2000s. While some aspects may be a bit outdated—given that the processes used in CGI studios have evolved considerably—I do plan to revisit this lesson in the future. However, it contains valuable information, both historical and practical, that can be useful for understanding the next lesson, "An Introduction to Lighting." Therefore, I have decided to republish it nonetheless (March 2024), prior to that planned update.

An introductory note: This lesson was initially written in the early 2000s, aimed at providing content for CG artists I was working with at the time. Many struggled with the concept of BRDFs and didn't understand the reasons behind certain requirements, such as why it was better to keep light intensity at 1 and use exposure to control light brightness. This approach, long utilized in pioneering studio pipelines like ILM and Weta, took time to be introduced into commercial rendering solutions such as Arnold. CG artists found it challenging to adopt this feature and change their habits accordingly. Questions arose like why we need to paint linear RGB values in textures, what this cumbersome term "BRDF" that we constantly use means, what reflectance and albedo are, and why we need to divide the albedo by $\pi$ for diffuse surfaces, etc.

This lesson is intended to demystify many of these concepts, especially for those artists. It tries to break down concepts and equations in a way that makes sense even to those with little mathematical background. As mentioned in the preamble, this content was written quite some time ago and, while accurate in principle, may not reflect current practices in studios. For instance, the use of chrome or grey balls has seen considerable improvements. I plan to revisit this in the future, but until then, we need to move forward with new content. I hope non-technical CG artists will find it valuable nonetheless in its current state.

What is a BRDF?

Many aspects of the CG lighting pipeline are mysterious to the people using it, such as how the brightness of an object relates to the intensity of a light. This chapter explains this relationship and introduces the concept of BRDF, which you may have heard often without really understanding what it means or how it works. In general, this lesson should lift the veil on a few similar, rather (what appears to be) mysterious topics.

Radiometry: Defining Relations between Light and Matter

The techniques we use to simulate how light in the real world interacts with objects are based on a series of measures defined in radiometry: the field that studies the measurements of electromagnetic radiation, including visible light.

To understand where these techniques come from and how they work, we will first look at these radiometric terms and explain how they relate to the physical world. From there, we will introduce the concepts of BRDF and albedo, and give an example of a BRDF for diffuse surfaces.

Radiometry Terms: Flux, Irradiance, and Radiance

Light can be seen as a collection of particles (photons) traveling in space, carrying energy. We model the photons' direction as a straight line. When we talk about the amount of light emitted by an object, the term actually relates to the quantity of photons that is emitted by an object. What interests us most in CG is the amount of light arriving at and leaving the surface of an object.

The first important notion is the light power, called flux, which is expressed in watts (W). The flux is a quantity of luminous energy (number of photons) passing through a surface per unit of time. Intuitively, one can see that the properties of a material, such as its color and brightness, have some form of relation with the ratio of the reflected flux (the amount of light that is reflected off the surface) to the incoming flux (the amount of light that arrived at the surface). A black surface should reflect no flux (no light), while a pure reflector should reflect all the incoming flux. In the real world, most objects' behavior lies somewhere in the middle.

$$\text{material brightness} = \frac{\text{light reflected}}{\text{light received}}$$

**Figure 1:** Flux measures the quantity of luminous energy passing through a surface per unit of time.

In the real world, the appearance of objects often varies across their surface. We describe their appearance as spatially variable. A prime example of such material is marble. Defining the flux reflected by a slate of marble requires a refined understanding of flux that incorporates the concept of locality. Rather than considering the flux that is received or reflected by a surface in its entirety, we examine the flux received and reflected at a specific point on the surface (let's denote this point as $x$). However, since a point cannot be physically defined in the real world, we instead consider a very small area around a point—so small that the surface of this area is guaranteed to have a consistent color. This very small surface is termed a differential area (Figure 2).

When described in relation to this differential area, we now view the flux as a density. The flux density arriving at a surface is named irradiance, while the flux density emitted from a point can be referred to as radiant exitance or radiosity, though the latter includes the sum of emitted (which we will currently ignore) and reflected flux density. Irradiance is measured in watts per square meter ($W/m^2$). Although a textured object (such as marble) may receive uniform irradiance across its surface, the reflected irradiance can vary spatially.

**Figure 2:** To measure the flux at a point, we need to consider a very small region around the point termed the differential area. Because this region is very small, there's no flux variation over its area.

Furthermore, most objects also exhibit view-dependent properties. For a given point on the surface, the reflected light changes with the viewing angle. The definition of irradiance does not account for any view-dependent behavior, thus necessitating a new quantity known as radiance, which is measured in watts per square meter per unit solid angle ($W/m^2\cdot sr^{-1}$). Radiance quantifies the light incoming at (or emitted from) a given point for a specific direction in space. The ratio of reflected radiance at a point into a given direction enables the description of almost any material.

Radiance in a direction can be visualized as a flux of photons passing through a cylinder of infinitesimal radius. It's important to note that the human eye itself is a surface; thus, in computer graphics, we use radiance to describe how light reflected by objects interacts with the surface responsible for creating an image.

Flux, irradiance, and radiance allow us to describe nearly every lighting phenomenon. With radiance as the foundational quantity, both irradiance and flux can be derived from it.

Short Introduction to the Radiometry Equations

Flux is denoted by $\phi$ and is expressed in W.

Irradiance is denoted by E and is expressed in $W \cdot m^{-2}$.

Radiance is denoted by L and is expressed in $W \cdot m^{-2} \cdot sr^{-1}$.

Radiometry bears similarity to the science of photometry, but photometry measures the brightness of lights as perceived by the human eye, while radiometry deals with absolute power values. Photometry is confined to light from the visible spectrum, whereas radiometry encompasses the entire spectrum.

As previously mentioned, points and directions are theoretical concepts that do not physically exist. A point on a surface typically refers to a very small area around that point. Similarly, a direction generally describes a very small angle around that direction, known as a differential solid angle. Irradiance at a point describes the flux passing through a very small element of the surface around the point. Radiance measures the flux passing through a very small area on the surface around $x$ into a very small cylinder (illustrated as a cone in figure 3 due to perspective) centered around a given direction. This notion of a small cylinder parallels the concept of a small area around $x$. We typically refer to this as a differential solid angle and use the Greek letter omega ($\omega$) to represent it: $d\omega$ or $d\Omega$.

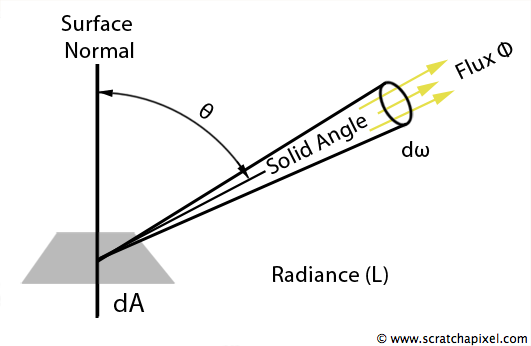
**Figure 3:** Radiance (L) measures the outgoing radiant flux per solid angle ($d\omega$ here represents a differential solid angle) per area projected ($dA \cos \theta$) onto the surface in the direction of radiation (the eye in our case).

Irradiance quantifies the incoming light at a given point, while radiance quantifies the incoming light at a given point from a specific direction. This implies that the total irradiance at point $x$ can be computed from the radiance by aggregating the radiance from all directions in the hemisphere oriented around the normal at $x$. If we consider radiance for just one incoming direction (rather than the entire hemisphere), we can calculate the corresponding fraction of irradiance, referred to as differential irradiance (denoted $dE$).

The figures illustrate that for a given radiance (photon flux through a small cylinder), the quantity of photons passing through a small element of the surface (our differential irradiance) depends on the angle of incidence of the cylinder. When the cylinder is perpendicular to the surface, all photons traveling through the cylinder strike the surface element. As the cylinder rotates, the intersection between the surface and the cylinder enlarges, meaning fewer photons pass through our original surface element. Ultimately, when the cylinder is parallel to the surface, no photons strike the surface element.

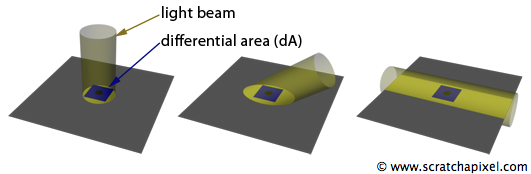
**Figure 4:** As the beam of light makes an angle with the plane, the surface covered by the beam increases. This means that the differential area (the blue square in this figure) receives fewer and fewer photons (the same number of photons is spread across a larger region) as the light angle of incidence increases. The light intensity can be multiplied by the cosine of the angle subtended by the light and the surface normal. This relation is known as the Lambert cosine law.

This relationship is known as the Lambert Cosine Law. To account for the reduced number of photons reaching the surface element as the angle between the normal at the surface and the light increases, we multiply the light energy by the cosine of this angle.

$$dE = \cos(\theta) L d\omega$$

Where $\theta$ is the angle of incidence, $L$ represents the radiance incoming along a direction, and $d\omega$ denotes the small cylinder centered along this direction, expressed with a differential solid angle.

To calculate the total irradiance, we employ a mathematical technique called integration to sum all the fractional irradiances for all directions in the hemisphere. This can be mathematically represented as follows:

$$E = \int\limits_\Omega dE = \int \limits_\Omega \cos(\theta) L d\omega$$

Properties of a Surface

Given the quantities introduced so far, we can now define the properties of a surface as ratios between incoming and reflected flux.

If this ratio equals 0, it implies that the surface reflects no light and appears totally black. A ratio of 1 indicates a purely reflective surface, meaning all incoming irradiance is reflected. This ratio cannot exceed 1, as that would imply the surface is generating light (excluding the consideration of emissive surfaces for now). A surface may reflect less light than it receives because some incoming light is absorbed by the material. This ratio, in essence, quantifies how much of the incoming light is absorbed by an object.

Let's now express this ratio in mathematical form for a beam of light (a single direction) arriving at point $x$ on the surface. Remember, when considering a single direction instead of all directions in the hemisphere, we focus on differential quantities. For a beam of light, this ratio is therefore between the differential incoming radiance (light coming in) with direction $\omega_i$ and the differential outgoing radiance in the direction of the observer (with direction $\omega_o$). This ratio is known as reflectance (denoted $f_r$) and is expressed as:

$$ f_r = \frac{dL(\omega_o)}{dE(\omega_i)} = \frac{dL(\omega_o)}{\cos(\theta_i) L(\omega_i) d\omega_i} $$

Given that $f_r$ depends on an incoming and an outgoing direction, it is inherently 4-dimensional (as directions are typically expressed in spherical coordinates). Reflectance is also referred to as the BRDF (Bidirectional Reflectance Distribution Function), which is dimensionless but is expressed in terms of $sr^{-1}$ (per steradian).

To compute the final color of a point as observed from a specific direction ($\omega_o$), we must calculate the total reflected radiance by summing all the differential radiance:

$$ \begin{aligned} dL(\omega_o) &= f_r dE(\omega_i) \\ L &= \int \limits_\Omega f_r dE(\omega_i) = \int \limits_\Omega f_r \cos(\theta_i) L(\omega_i) d\omega_i \end{aligned} $$

A BRDF for a Diffuse Surface

To simplify the case, let's consider only a purely diffuse material. "Purely diffuse" means that the material reflects light uniformly in all directions within the hemisphere, and its reflectance is constant. Because it is constant, we can take $f_r$ out of the integral. The previous equations can then be simplified to:

$$ L(\omega_o) = \int \limits_\Omega f_r \cos(\theta_i)L(\omega_i)d\omega_i = f_r \int \limits_\Omega \cos(\theta_i)L(\omega_i)d\omega_i = f_rE $$

Remember, $E$ is the total irradiance. Let's consider that the incoming radiance (irradiance) is constant over the hemisphere, that is, $L(\omega_i) = 1$. Reflected radiance in any direction can then be expressed as:

$$ L(\omega_o) = f_r \int \limits_\Omega \cos(\theta_i)d\omega_i = f_r\pi $$

This integral resolves to $\pi$ in that particular case. Readers interested in how we arrived at this result can find the mathematical derivation in the following note (this note itself takes some shortcuts. Check the lesson on BRDFs in the basic section for a full introduction to the topic).

$$ \begin{equation} \begin{array}{ll} \displaystyle\int_{\Omega^+} \cos(\theta) d\omega & \quad (1) \\ \displaystyle\int_{\theta=0}^{\frac{\pi}{2}} \int_{\phi=0}^{2\pi} \cos(\theta) \sin(\theta) d\phi d\theta & \quad (2) \\ \displaystyle 2\pi \int_{\theta=0}^{\frac{\pi}{2}} \cos(\theta) \sin(\theta) d\theta & \quad (3) \\ \displaystyle\int_{\theta=0}^{\frac{\pi}{2}} \cos(\theta) \sin(\theta) d\theta = \left[-\frac{1}{2}\cos^2(\theta)\right]_{\theta=0}^{\frac{\pi}{2}} & \quad (4) \\ \displaystyle\int_{a}^{b} f(x) dx = F(b) - F(a) & \quad (5) \\ \displaystyle\frac{1}{2} \left[ \cos^2\left(\frac{\pi}{2}\right) - \cos^2(0) \right] = 0 - \frac{1}{2} - \frac{1}{2} = -\frac{1}{2} & \quad (6) \\ \displaystyle\int_{\Omega} \cos(\theta) d\omega = 2\pi \frac{1}{2} = \pi & \quad (7) \end{array} \end{equation} $$

Equation 1 represents how we have defined the integral of the function $\cos(\theta)$ so far. This equation can be rewritten in a more classical form (2), where the integral over the solid angle $d\omega$ can be rewritten as two integrals: $d\omega$ is replaced by $\sin(\theta)d\theta d\Phi$, $\theta$ is in the range $[0, \pi/2]$, and $\Phi$ is in the range $[0, 2\pi]$. The integration of $\Phi$ gives $2\pi$. The remaining integral, which includes the original function $\cos(\theta)$, can be rewritten using what's known in calculus as the definite integral. In short, if $F(x)$ is the primitive function of $f(x)$ (or if $f(x)$ is the derivative of $F(x)$), then you can write that the integral of $f(x)$ in the range $[a, b]$ is equal to $F(b) - F(a)$ (equation 5). Equation 4 shows what the primitive function of $\cos(\theta)\sin(\theta)$ is. We then apply equation 5 using this primitive function ($-\frac{1}{2}\cos^2(x)$) to find the value $\frac{1}{2}$ ($a=0$ and $b=\pi/2$). Finally, we multiply $2\pi$ by $\frac{1}{2}$ which gives us $\pi$.

Just in case you didn't understand how the antiderivative was determined, here are the steps. We will start from the antiderivative and demonstrate that its derivative is indeed $\cos(\theta) \sin(\theta)$:

1. Starting with: $\frac{1}{2}\left(-\frac{d}{dx}(\cos^2x)\right)$

2. Let: Define $u = \cos x$. This leads us to consider: $-\frac{1}{2}\frac{d}{dx}(u^2)$

3. Apply the Chain Rule: To derive $\frac{d}{dx}(u^2)$, we utilize the chain rule. This rule stipulates that to differentiate a composite function, you first differentiate the outer function treating the inner function as a variable, and then multiply by the derivative of the inner function with respect to $x$.

4. Chain Rule in Action:

Differentiating $u^2$ with respect to $u$ yields $2u^{2-1} = 2u$.
The derivative of $u$ with respect to $x$, given $u = \cos x$, is $\frac{d}{dx}(\cos x) = -\sin x$.

5. Combining the Results:

Thus, $\frac{d}{dx}(u^2) = 2u \cdot \frac{d}{dx}u = 2\cos x \cdot (-\sin x)$.

6. Final Step:

By substituting back into the original expression, we find: $\frac{1}{2}\left(-2\cos x (-\sin x)\right) = \cos x \sin x$.

Therefore, if we're considering a diffuse material with a constant BRDF $f_r$, illuminated with a constant radiance of 1, the reflected radiance in all directions is $\pi f_r$. In the case where the amount of incident light is 1 and $f_r$ is 1, the amount of reflected light is $\pi$, which means that the surface creates energy. In order to have a physically plausible result (energy conserving), the reflected light in this case should not be greater than 1. Therefore, $f_r$, the BRDF for a diffuse surface, needs to be:

$$\text{BRDF diffuse} = \frac{k}{\pi}$$

The term $k$, which is in the range $0$ to $1$, is usually called albedo.

From a lighting perspective, this means that if $k$ is $1$ for an object illuminated by a distant light perpendicular to the surface (so that there is no attenuation due to the Lambert law), the reflected value should be $\frac{1}{\pi}$.

Conversely, if you illuminate the same object with a dome light that has a constant radiance of $1$, we will have to compute the total incoming irradiance over the hemisphere by integrating the differential incoming irradiance. This involves solving for the equation introduced earlier:

$$E = \int \limits_\Omega dE = \int \limits_\Omega \cos(\theta)Ld\omega$$

This equation is similar to the one we just solved. Assuming $L = 1$, we integrate and find that $E = \pi$. Therefore, when you multiply $\pi$ by a diffuse BRDF with a constant $k$ that equals $1$, you get $1$. When $k$ equals $1$ and the surface is illuminated by a dome light of constant radiance $1$, the brightness of the surface is $1$. In computer graphics and rendering, we call this setup the furnace test.