Global Illumination and Path Tracing

Global Illumination and Path Tracing: a Practical Implementation

Reading time: 36 mins.

Global Illumination in Practice: Monte Carlo Path Tracing

In the previous chapter, we introduced the principle of Monte Carlo integration to simulate global illumination. We also explained that uniformly sampling the hemisphere works well for simulating indirect diffuse lighting but not for simulating indirect specular reflections or caustics. For this reason, we will limit ourselves to simulating indirect diffuse lighting in this lesson. Diffuse objects illuminate each other as an "indirect" effect, with these objects reflecting light and thus acting, in a sense, as sources of light.

In the first chapter, we demonstrated how the Monte Carlo integration method works in 2D. Extending the technique to 3D is relatively "simple" and works on the same principle. Here are the steps, which are quite similar to those we followed in the 2D case.

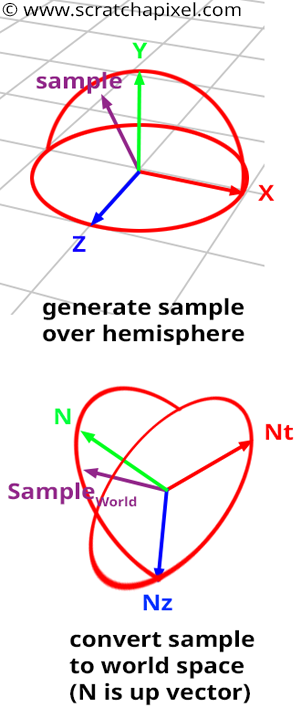
**Figure 1:** Transforming samples from the coordinate system in which they were created to world space (in the shaded point’s local coordinate system, where the up vector is aligned with $N$).

Concept: Ideally, we want to create samples on the hemisphere oriented around the normal $N$ of the shaded point $P$. However, as in the 2D case, it is easier to create these samples in a hemisphere oriented along the y-axis of a "canonical" Cartesian coordinate system, then transform them into the shaded point’s local coordinate system (where the hemisphere is oriented along the normal, as shown in Figure 1 - bottom). We prefer to create samples in a hemisphere with an up vector aligned with the y-axis of the world Cartesian coordinate system because the sample coordinates in this system can be easily computed with basic spherical-to-Cartesian coordinate equations:

$$ \begin{array}{l} x = \sin \theta \cos \phi,\\ y = \cos \theta,\\ z = \sin \theta \sin \phi,\\ \end{array} $$

These coordinates are then transformed into the shaded point’s local coordinate system. In this lesson, we will explain how to create samples, establish a new coordinate system where the shading normal $N$ defines the up axis, and compute the other axes of this local Cartesian coordinate system (which are tangent to the surface at $P$ and perpendicular to $N$). If you read the lesson on Geometry, you should know that once we have the axes of an orthogonal coordinate system $C$, we can transform any point or vector (i.e., direction) from any Cartesian coordinate system to $C$.

**Figure 2:** The principle of Monte Carlo integration applied to a 3D scene. Rays are randomly generated within a hemisphere of directions oriented around the shading normal $N$. If these rays hit an object, the color at the intersection point is computed and returned to the shading point. All colors are summed and divided by the number $N$ of cast samples. Monte Carlo theory also implies dividing each sample by the PDF of the random variable. Additionally, we multiply the object's color by the cosine of the angle between the shading normal and the ray direction (here, the light direction).

Step 1: Create a Cartesian coordinate system where the up vector is aligned with the shaded point’s normal $N$.
Step 2: Create a sample using the spherical-to-Cartesian coordinate equations. We will demonstrate how to do this in practice in this chapter.
Step 3: Transform the sample direction from the original coordinate system to the shaded point’s coordinate system.
Step 4: Trace a ray into the scene in the sampled direction.
Step 5: If the ray intersects an object, compute the color of the object at the intersection point and add this result to a temporary variable. Since the surface is diffuse, don’t forget to multiply the light intensity returned along each ray by the dot product between the ray direction (the light direction) and the shaded normal $N$ (see below).
Step 6: Repeat steps 2 to 5, $N$ times.
Step 7: Divide the temporary variable that holds the results of all sampled rays by $N$, the total number of samples. This final value approximates the shaded point’s indirect diffuse illumination: the illumination of $P$ by other diffuse surfaces in the scene.

Remember that we need to divide each sample contribution by the PDF of the random sample. This will be explained later in this chapter.

In pseudo-code, we get:

Vec3f castRay(Vec3f &orig, Vec3f &dir, const uint32_t &depth, ...)
{
    if (depth > options.maxDepth) return 0;
    Vec3f hitPointColor = 0;
    // compute direct lighting
    ...
    // Step 1: compute the shaded point coordinate system using normal N.
    ...
    // number of samples N
    uint32_t N = 16;
    Vec3f indirectDiffuse = 0;
    for (uint32_t i = 0; i < N; ++i) {
        // Step 2: create a sample in world space
        Vec3f sample = ...;
        // Step 3: transform sample from world space to the shaded point’s local coordinate system
        sampleWorld = ...;
        // Steps 4 & 5: cast a ray in this direction
        indirectDiffuse += N.dotProduct(sampleWorld) * castRay(P, sampleWorld, depth + 1, ...);
    }
    // Step 7: divide the sum by the total number of samples N
    hitPointColor += (indirectDiffuse / N) * albedo;
    ...
    return hitPointColor;
}

What castRay essentially does is return the amount of light that an object reflects toward the shaded point along the direction sampleWorld (if the ray intersects an object). The principle used to compute this light ray’s contribution to the color of $P$ is the same as with standard light sources. In other words, if the surface is diffuse, we should multiply the light intensity by the cosine of the angle between the light direction (sampleWorld) and the shading normal $N$.

Next, let’s go through the implementation of these steps one by one.

Step 1: Create a Local Coordinate System Oriented Along the Shading Normal $N$

We want to build a Cartesian coordinate system in which the normal $N$ is aligned with the system’s up vector (or y-axis). From the lesson on Geometry, we know that a vector can also be interpreted as the coefficients of a plane equation, and that this plane is perpendicular to the vector:

$$ \begin{array}{l} A * x + B * y + C * z = D = 0,\\ N_x * x + N_y * y + N_z * z = D = 0. \end{array} $$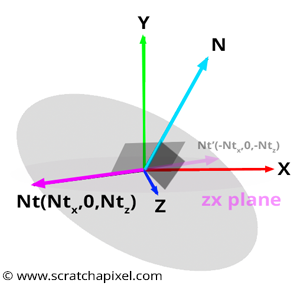

**Figure 3:** Two vectors lying in the plane perpendicular to the normal $N$ exist.

Since we are working with vectors (not points), the plane passes through the world origin, so we can set $D = 0$. To build a Cartesian coordinate system, we can assume that any vector on this plane is perpendicular to $N$. Let’s call this vector $N_T$. We can use $N_T$ as the second axis of our coordinate system. By taking the cross product of $N_T$ and $N$, we create a third vector, $N_B$, which is perpendicular to both $N_T$ and $N$. Voilà! $N$, $N_T$, and $N_B$ now form a Cartesian coordinate system. So how do we find a vector lying in the plane?

In Figure 3, you’ll notice that one vector in the plane has its y-coordinate equal to 0. Therefore, we can assume there is a vector in this plane with a y-coordinate of 0, which reduces our plane equation to two unknowns:

$$N_x * x + N_y * (y = 0) + N_z * z = N_x * x + N_z * z = 0.$$

We can rewrite this equation as:

$$N_x * x = - N_z * z.$$

This equation holds if $x = N_z$ and $z = -N_x$ or if $x = -N_z$ and $z = N_x$. Thus, if we take either $N_T = \{N_z, 0, -N_x\}$ or $N_T = \{-N_z, 0, N_x\}$, we obtain a vector lying in the plane perpendicular to $N$. Either option works, as long as we create a right-hand coordinate system, which also depends on the order in which we arrange $N$ and $N_T$ in the final cross product. The only detail left is to normalize $N_T$:

void createCoordinateSystem(const Vec3f &N, Vec3f &Nt, Vec3f &Nb)
{
    Nt = Vec3f(N.z, 0, -N.x) / sqrtf(N.x * N.x + N.z * N.z);
    ...
}

Finally, we compute $N_B$ using the cross product:

void createCoordinateSystem(const Vec3f &N, Vec3f &Nt, Vec3f &Nb)
{
    Nt = Vec3f(N.z, 0, -N.x) / sqrtf(N.x * N.x + N.z * N.z);
    Nb = N.crossProduct(Nt); 
}

However, if the y-coordinate of the normal vector $N$ is greater than its x-coordinate, this approach may not be numerically robust. In such cases, it’s better to build a vector within the plane with an x-coordinate of 0. Referring to Figure 3, we see that this is also an option:

$$N_x * (x = 0) + N_y * y + N_z * z = N_y * y + N_z * z = 0.$$

Using the same logic, we can find suitable values for $y$ and $z$. Finally, we arrive at:

void createCoordinateSystem(const Vec3f &N, Vec3f &Nt, Vec3f &Nb) 
{ 
    if (std::fabs(N.x) > std::fabs(N.y))
        Nt = Vec3f(N.z, 0, -N.x) / sqrtf(N.x * N.x + N.z * N.z);
    else
        Nt = Vec3f(0, -N.z, N.y) / sqrtf(N.y * N.y + N.z * N.z);
    Nb = N.crossProduct(Nt); 
}

Our local coordinate system is now complete! Next, we’ll learn how to create samples and transform these samples in this coordinate system.

Create Samples on the Hemisphere

**Figure 4:** The amount of light reflected by objects in the scene toward $P$, the shading point, can be described as a function of the solid angle, which can also be expressed in terms of spherical coordinates. In the 2D case, it is just a function of the angle $\theta$. This is the function we want to integrate over all directions within a half-disk in 2D or a hemisphere in 3D.

As you know, we can define the position of a point on the sphere (or hemisphere) using either polar coordinates or Cartesian coordinates. In polar coordinates, a point or a vector (here, we are interested in direction) is defined with two angles: $\theta$ (the Greek letter theta) and $\phi$ (the Greek letter phi). The first angle, $\theta$, is in the range $[0,\pi/2]$, and the second angle, $\phi$, is in the range $[0,2\pi]$. Remember, the Monte Carlo integration method works if we choose sample directions randomly.

This is where Monte Carlo theory comes in. What we want to do is uniformly sample the hemisphere with respect to the solid angle. We won’t go over Monte Carlo theory again here, so if you haven’t read it, now would be a good time to review it in the Mathematical Foundations of Monte Carlo Methods and Monte Carlo in Practice lessons. Ready? Let’s dive into the math.

The equation we’ll use, called an estimator, looks like this:

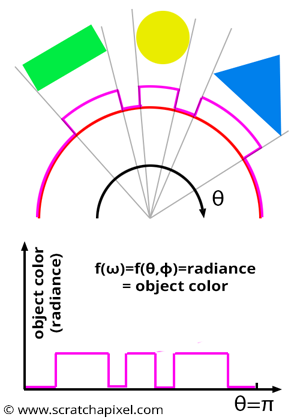
$$\langle F^N \rangle = \dfrac{1}{N} \sum_{i=0}^{N-1} \dfrac{f(X_i)}{pdf(X_i)}.$$

This is the general form of a Monte Carlo estimator used to approximate an integral. In this case, what we want to integrate is the function $f(x)$. As explained in the previous chapter, this function represents the amount of light arriving at $P$, the shaded point, from all directions in the hemisphere oriented around $P$’s normal. It may help to imagine this function in 2D (or as a slice through the hemisphere), as shown in Figure 4. Here, we want to sample this function for random directions. In the equation, this is represented by the random variable $X_i$. So, the idea is to generate a random direction $D_R$ in the hemisphere and evaluate the function in that direction, which means “cast a ray from $P$ in the direction $D_R$ into the scene and return the color of the object the ray intersects (if it intersects an object).” That color represents the amount of light that the intersected object reflects toward $P$ along the ray direction $D_R$.

Mathematically, we also need to divide this result by the probability of generating the direction $D_R$, represented in the equation by the term called PDF (probability density function). Each random direction $X_i$ can have a unique result for this function, which is why it is expressed as a function. However, since we want to generate uniformly distributed samples (or directions), all the rays will have the same PDF. In this case, the PDF is constant because every ray or direction has the same probability of being generated (equiprobability). Now let’s find this PDF and learn how to generate these random, uniformly distributed samples or directions.

To sample a function, we first need to find its PDF, then compute its cumulative distribution function (CDF), and finally, the inverse of the CDF. These steps are covered in detail in the lesson on the Mathematical Foundations of Monte Carlo Methods. Keep in mind that we want to sample the hemisphere uniformly, meaning that each sample or direction should have the same probability as any other. The probability of selecting any direction—whether $A$, $B$, $C$, or $D$—is given by the function’s PDF. All PDFs must integrate to 1 over their sample space (or domain of integration). For the hemisphere, we’ll define this sample space in terms of the solid angle, which is equal to $2\pi$ for a hemisphere. Since every sample has an equal probability of being generated, our PDF will be constant. If we write the PDF as $p(x)$ and integrate it over the entire sample space ($2 \pi$), we get:

$$\int_{\omega = 0}^{2\pi} p(\omega) \, d \omega = 1.$$

Because, as mentioned before, a PDF must integrate to 1 over the function’s sample space. Since $p(\omega)$ is constant, we can write (replacing the PDF with the constant $C$ in the equation):

$$C \int_{\omega = 0}^{2\pi} \, d\omega = 1.$$

We know (see the lesson on the Mathematics of Shading in the Mathematics of Computer Graphics section) that:

$$\int_{x=a}^b \, dx = b - a.$$

Thus:

$$C * \int_{\omega = 0}^{2\pi} \, d\omega = C * (2\pi - 0) = 1.$$

From this, we can find $C$, or the PDF of our function:

$$C = p(\omega) = \dfrac{1}{2\pi}.$$

So far, so good. Knowing the PDF of the function we want to sample is a good start, but we can’t work with solid angles directly. Our ultimate goal is to generate random directions within the hemisphere, so we need to express this PDF in terms of polar coordinates, i.e., in terms of $\theta$ and $\phi$:

Now, we know that the probability of a given solid angle belonging to a larger set can be written as:

$$Pr(\omega \in \Omega) = \int_\Omega p(\omega) \, d\omega.$$

This generalizes the equation we integrated above, where $\omega$ was equal to $2\pi$, covering the entire hemisphere. Now, to express the probability density function in terms of $\theta$ and $\phi$, we write:

$$p(\theta, \phi) \, d\theta \, d\phi = p(\omega) \, d\omega.$$

In the previous lesson, we learned that a differential solid angle can be rewritten in terms of polar coordinates as follows:

$$d \omega = \sin \theta \, d \theta \, d \phi.$$

Substituting this in the previous equation, we get:

$$ \begin{array}{l} p(\theta, \phi) \, d\theta \, d\phi = p(\omega) \, d\omega, \\ p(\theta, \phi) \, d\theta \, d\phi = p(\omega) \, \sin \theta \, d \theta \, d \phi. \end{array} $$

The $d \theta$ and $d \phi$ terms on each side cancel out, giving us:

$$ \begin{array}{l} p(\theta, \phi) = p(\omega) \, \sin \theta, \\ p(\theta, \phi) = \dfrac{\sin \theta}{2 \pi}. \end{array} $$

Here, we replaced $p(\omega)$ with the value we computed above: $p(\omega) = 1 / 2\pi$. We’re almost there. The function $p(\theta, \phi)$ is called a joint probability distribution. Now, we need to sample $\theta$ and $\phi$ independently. In this case, the PDF is separable: we can split the PDF into two PDFs, one for $\theta$ and one for $\phi$. Another way to achieve this is by using marginal and conditional PDFs. A marginal distribution is one in which the probability of a given variable (e.g., $\theta$) is expressed without reference to other variables (e.g., $\phi$). This can be done by integrating the joint PDF with respect to one of the variables. In our case, we get (integrating $p(\theta, \phi)$ with respect to $\phi$):

$$ p(\theta) = \int_{\phi=0}^{2 \pi} p(\theta, \phi) \, d \phi = \int_{\phi=0}^{2 \pi} \dfrac{\sin \theta}{2 \pi} \, d\phi = 2\pi * \dfrac{\sin \theta}{2 \pi} = \sin \theta. $$

The conditional probability function provides the probability function of one variable (e.g., $\phi$) given that the other variable ($\theta$) is known. For continuous functions (like our PDFs), this can be computed as the joint probability distribution $p(\theta, \phi)$ over the marginal distribution $p(\theta)$:

$$p(\phi) = \dfrac{ p(\theta, \phi) }{ p(\theta) } = \dfrac{1}{2\pi}.$$

Now that we have the PDFs for $\theta$ and $\phi$, we need to find their respective CDFs (and their inverses). Recall from the Monte Carlo lesson that a CDF represents the probability that a random variable $X$ has a value less than or equal to $x$. For example, we could ask, "If we randomly generate a value for $\theta$, what’s the probability that $\theta$ is less than or equal to $\pi/4$?" We can compute this CDF by integrating the PDF:

$$Pr(X \leq \theta) = P(\theta) = \int_0^\theta p(\theta) \, d\theta = \int_0^\theta \sin \theta \, d\theta.$$

The Fundamental Theorem of Calculus states that if $f (x)$ is continuous on $[a, b]$ and if $F(x)$ is any antiderivative of $f(x)$, then

$$\int_{a}^{b} f(x) \, dx = F(b) - F(a).$$

The antiderivative of $\sin x$ is $-\cos x$, so:

$$\int_0^\theta \sin \theta \, d\theta = \left [ -\cos \theta \right ]_0^{\theta} = \left [-\cos \theta - - \cos 0 \right ] = 1 - \cos \theta.$$

The CDF of $p(\phi)$ is simpler:

$$Pr(X \leq \phi) = P(\phi) = \int_0^\phi \dfrac{1}{2\pi} \, d \phi = \dfrac{1}{2\pi} \left [ \phi - 0 \right ] = \dfrac{\phi}{2 \pi}.$$

Let’s invert these CDFs:

$$ \begin{array}{l} y = 1 - \cos \theta, \\ \cos \theta = 1 - y, \\ \theta = \cos^{-1}(1-y). \end{array} $$ $$ \begin{array}{l} y = \dfrac{\phi}{2 \pi}, \\ \phi = y * 2 \pi. \end{array} $$

Congratulations! According to Monte Carlo theory, if we draw some random variables uniformly distributed in the range $[0,1]$, then replace these random numbers in the equations above, we obtain uniformly distributed values of $\theta$ and $\phi$, which we can use in the polar-to-Cartesian coordinates equations to compute a random, uniformly distributed direction over the hemisphere. Here’s how this works in practice:

Vec3f uniformSampleHemisphere(const float &r1, const float &r2)
{
    // cos(theta) = r1 = y
    // cos^2(theta) + sin^2(theta) = 1 -> sin(theta) = sqrtf(1 - cos^2(theta))
    float sinTheta = sqrtf(1 - r1 * r1);
    float phi = 2 * M_PI * r2;
    float x = sinTheta * cosf(phi);
    float z = sinTheta * sinf(phi);
    return Vec3f(x, r1, z);
}

...
std::default_random_engine generator;
std::uniform_real_distribution<float> distribution(0, 1);

uint32_t N = 16;

for (uint32_t n = 0; n < N; ++n) {
    float r1 = distribution(generator);
    float r2 = distribution(generator);
    Vec3f sample = uniformSampleHemisphere(r1, r2);
    ...
}

A couple of interesting points about the code above: when we inverted the first CDF, one of the equations was $\cos \theta = 1 - y$. Here, $y$ is the random variable uniformly distributed between 0 and 1 that we use to randomly pick a value for $\theta$. Thus, $1 - y$, or $1 - \epsilon$ (where $\epsilon$, the Greek letter epsilon, represents our uniformly distributed random variable) is equal to $\cos \theta$. Note that $\cos \theta$ is the y-coordinate of the random direction, so we can directly set the y-coordinate with $1 - \epsilon$ (line 9). Also, since $\cos^2 \theta + \sin^2 \theta = 1$, we get $\sin \theta = \sqrt{1 - \cos^2 \theta}$. Replacing $\cos \theta$ with $1 - \epsilon$, we find $\sin \theta = \sqrt{1 - (1-\epsilon)^2}$. Since $\epsilon$ is uniformly distributed, using $1-\epsilon$ or $\epsilon$ yields the same result; either can be used interchangeably.

That’s a lot of math, but now you know how to generate uniformly distributed random samples on the hemisphere. Let’s move to the next step and transform this sample to the shaded point’s local coordinate system.

Step 3: Transform the Random Samples to the Shaded Point’s Local Coordinate System

We have already computed a local Cartesian coordinate system where the normal of the shaded point is aligned with the up vector of this coordinate system. As we learned in the lesson on geometry, the three vectors of this Cartesian coordinate system can be used to build a 4x4 matrix (or a 3x3 matrix if we only care about directions). This matrix transforms a direction from its initial space to the coordinate system from which we built the transformation matrix.

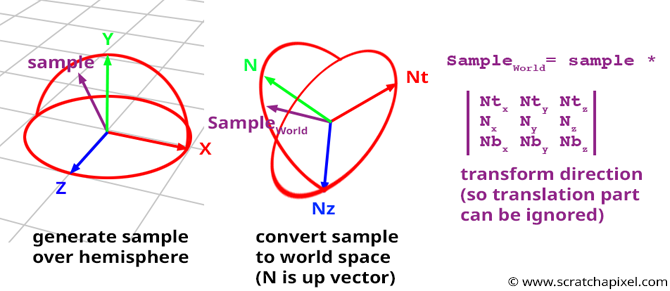
In this particular case, we will use the vectors of the Cartesian coordinate system directly without building an explicit matrix (if you’re uncertain about this part of the code, we recommend reviewing the lesson on Geometry):

Vec3f Nt, Nb;

createCoordinateSystem(hitNormal, Nt, Nb);

for (uint32_t n = 0; n < N; ++n) {
    float r1 = distribution(generator); // cos(theta) = N.Light Direction
    float r2 = distribution(generator);
    Vec3f sample = uniformSampleHemisphere(r1, r2);
    Vec3f sampleWorld( 
        sample.x * Nb.x + sample.y * hitNormal.x + sample.z * Nt.x,
        sample.x * Nb.y + sample.y * hitNormal.y + sample.z * Nt.y,
        sample.x * Nb.z + sample.y * hitNormal.z + sample.z * Nt.z);
    ...
}

Remember that the shading normal $N$ serves as the up vector (the y-axis) in this coordinate system. If you look at how we generated $N_t$ and $N_b$ in the createCoordinateSystem function, you’ll see that when the shading normal is equal to (0,1,0), $N_t$ aligns with the positive x-axis, and $N_b$ aligns with the positive z-axis.

Steps 4, 5, and 6: Trace the Indirect Rays

The next step is to trace each ray and accumulate the returned color into a temporary variable. Once all rays have been traced, we divide this temporary variable (which holds the accumulated light from each indirect cast ray) by $N$, the total number of samples.

Vec3f indirectDiffuse = 0;
for (uint32_t n = 0; n < N; ++n) {
    float r1 = distribution(generator); // cos(theta) = N.Light Direction
    float r2 = distribution(generator);
    Vec3f sample = uniformSampleHemisphere(r1, r2);
    ...
    // Don't forget to apply the cosine law (i.e., multiply by cos(theta) = r1).
    // We should also divide the result by the PDF (1 / (2 * M_PI)), but we can do this after
    indirectDiffuse += r1 * castRay(hitPoint + sampleWorld * options.bias, 
        sampleWorld, depth + 1, ...);
}
// Divide by N and the constant PDF
indirectDiffuse /= N * (1 / (2 * M_PI));

Remember, the light intensity returned along the direction sampleWorld also needs to be multiplied by the cosine of the angle between the shading normal and the light direction (which is the ray direction in this case). Since our object is diffuse, we need to apply the cosine law (introduced in the first lesson on shading). Note that the random variable r1 equals $\cos \theta$, which is the cosine of the angle between $N$ and the ray direction (see the uniformSampleHemisphere function code). So all we need to do here is multiply the result of castRay (the amount of light reaching $P$ from the direction sampleWorld) by r1 (line 8).

The general equation we’re trying to solve with this basic Monte Carlo integration is:

$$L(P) = \int_{\Omega_N} L(\omega_i) \, BRDF(P, \omega_i, \omega_o) \, \cos(\omega_i, N) \, d \omega = \color{red}{\int_{\Omega_N} L(\omega_i) \, \dfrac{\rho}{\pi} \, \cos(\omega_i, N) \, d \omega}$$

This simplified equation is what we call the rendering equation in computer graphics. We’ll introduce this fundamental equation more formally in the upcoming lessons. The term $L(P)$ on the left represents the color of point $P$, which we aim to compute. Technically, this is the radiance at $P$. On the right side of the equation, the integral sign indicates the domain of integration over the hemisphere of directions oriented around the surface normal. Here, we work with solid angles.

The term $L(\omega_i)$ is the light illuminating $P$ from direction $\omega_i$, and the BRDF describes the surface properties at $P$. For a diffuse surface, the BRDF is $\rho/\pi$, where $\rho$ is the surface albedo or color. Diffuse surfaces are view-independent, meaning the result of this function doesn’t depend on incoming light and view directions. However, for most BRDFs, the result does depend on these variables, which is why we pass them to the function. Finally, the cosine law term, $\cos(\omega_i, N)$, attenuates the BRDF result based on the angle between the incident light direction and the surface normal.

In this equation, we can easily calculate the BRDF of the shading point and the cosine term by accessing the scene data. The unknown term, $L(\omega_i)$, is evaluated by tracing a ray in the scene.

This is a more formal and compact way of expressing the problem we’re solving. We’ll revisit this equation in later lessons.

This is also where we divide the result of castRay by the random variable PDF, which, as shown earlier, is $1/(2\pi)$. Since the PDF is a constant, we don’t need to perform this division for each ray (or sample). Instead, we can do it after the loop (line 13). We’ll show later that this can be simplified even further. But don’t forget to divide by the PDF!

Step 7: Add the Indirect Diffuse Contribution to the Shaded Point’s Illumination

Finally, add the result of the indirect diffuse calculation to the total illumination of the shaded point and multiply the sum of the direct and indirect illumination by the object albedo.

hitColor = (directDiffuse + indirectDiffuse) * object->albedo / M_PI;

Remember, the BRDF of a diffuse surface is $\rho/\pi$, where $\rho$ represents the surface albedo. So we need to divide by $\pi$. For the indirect diffuse component, don’t forget that we should have divided the result of castRay by the PDF of the random variable, which we previously determined to be $1/(2\pi)$. Dividing indirectDiffuse by $1/(2\pi)$ is the same as multiplying by $2\pi$. And since the albedo is also divided by $\pi$, we can simplify the code above as follows:

// (indirectDiffuse / (1 / (2 * M_PI)) + directDiffuse) * albedo / M_PI
// (2 * M_PI * indirectDiffuse + directDiffuse) * albedo / M_PI
// (2 * indirectDiffuse + directDiffuse / M_PI) * albedo
hitColor = (directDiffuse / M_PI + 2 * indirectDiffuse) * object->albedo;

Et voilà!

Question From a Reader: Why Don’t We Use Spherical Attenuation Calculations (e.g., Dividing by the Square of the Distance) as We Do with Direct Light?

Here is the original question:

Spherical attenuation calculations (dividing by the square of the distance) are applied when sampling direct light but not for the transmission of indirect light. Why, then, is this calculation unnecessary for indirect light transmission?

This is a great question, though one you should be able to answer yourself after reading both this lesson and the lesson on Introduction to Lighting. However, we understand that this knowledge takes time to digest, so some readers will find this extended explanation very helpful here.

First of all, the question is not entirely accurate. The square falloff attenuation factor is applied only when dealing with spherical delta lights (e.g., point lights or spotlights). It doesn’t apply to all types of direct lights. For example, distant lights are not affected by the square falloff factor. Also, if you’ve read the lesson on area lights, you may have noticed that we don’t apply square falloff to area lights either. So, the square falloff factor only concerns point and spotlight sources, which, if you recall from the lesson devoted to lights, are defined as delta lights.

Why delta lights? Because, as mentioned in that lesson, they have no "physical size" in the scene. In other words, these lights are not represented by any shapes, and as a result, we need to compensate for the lack of shape by using equations that mimic the behavior of lights with physical shapes. In the real world, lights have physical dimensions, and due to this, light exhibits a falloff proportional to the square of the distance between the illuminated point and the light source's position.

That’s why we simulate square falloff when dealing with point and spot delta lights types.
And that’s why it’s not necessary to account for square falloff when dealing with area lights—lights that are represented by a shape, whether it’s a sphere, disk, rectangle, triangle, or a mesh made of triangles.

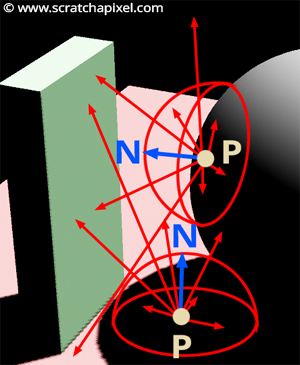
Now, the follow-up question you may have is: why or how is the square falloff accounted for when dealing with area lights? The key observation here is that every object in the scene reflects light and can, therefore, be considered a kind of area light—so what applies to area lights also applies when simulating indirect illumination/diffuse lighting.

The best way to develop an intuition for this is to look at the following images, where a spherical area light illuminates a point. In the left image, the spherical luminaire is 2 units away from $x$. In the right image, the sphere is 4 units away. As we sample the hemisphere above $x$ (256 rays are cast into the scene), you can see that far fewer rays are hitting the luminaire in the right image than in the left image (38 vs. 86 to be precise), where the luminaire is closer to $x$.

This obviously makes sense, but the key idea is that the number of rays hitting the luminaire decreases as the distance between $x$ and the luminaire increases. This naturally "encodes" the square falloff when dealing with area lights (within the context of ray/path tracing), since there's a direct relationship between the number of rays hitting the luminaire and the luminaire's contribution. The fewer the rays, the smaller the contribution.

Again, this provides the intuition as to why "we don't need to explicitly" account for the distance square falloff when the lights in the scene are area lights. Using area lights is what you should aim for if you can afford them over delta lights, such as point and spotlights, as they don't require artificially accounting for the distance square falloff. This is necessary for delta lights due to their lack of shape or size (recall that delta lights were only invented because, in the early days of computer graphics, simulating area lights (and indirect illumination/diffuse even more so) was too computationally expensive).

Note, by the way, that some DCC tools offer ways to customize the falloff to be something other than a power of 2, providing artists with creative control but leading to results that are not physically plausible.

Hope this makes sense and answers your question clearly.

Monte Carlo Path Tracing: Results

Let’s look at some results. You can find the source code used to render the scene below in the last chapter of this lesson (as usual). In the image below, there are two renders: on the left, global illumination is turned off, and on the right, it is turned on. Arrows indicate parts of the image where the effect of surfaces illuminating other objects can be observed, such as the floor affecting the bottom right of the sphere or the green monolith affecting the left side of the sphere. Notice how the sphere takes on the red or green hue of the floor and the monolith. This phenomenon, where the color of objects “bleeds” onto others, is commonly called color bleeding.

Render time is already significantly slower compared to rendering direct lighting alone. In this example, we’ve limited the number of bounces to 1; feel free to experiment with a higher number of bounces (if you’re patient enough to wait for the result).

Monte Carlo Path Tracing is Slow and Noisy

As shown in the images below, Monte Carlo path tracing produces noisy images. This is a major drawback of the technique. Why does this happen? If we go back to our poll example, imagine you choose a sample of 1,000 different people to estimate the average weight of a population. Each time you run the poll, you are likely to get a different group of 1,000 people. Consequently, each time you calculate the average of a new sample, you will get a slightly different result. This variation between the exact result (our goal with the integral) and the result from the Monte Carlo approximation (just an estimate) is what creates noise in the image.

The extent of this variation depends primarily on the sample size, $N$. By increasing $N$, we can reduce the noise in the image. The images above show a close-up of the sphere with different values of $N$. As $N$ increases, the noise becomes less visible. However, this comes at a cost, as rendering time increases with the number of samples. Monte Carlo theory tells us that to reduce noise (or variance) by half, we need four times more samples than originally used. For example, to reduce the noise of the first image on the left by half, you wouldn’t need 32 samples but rather 128, and to halve the noise in an image rendered with 128 samples, you would need 512 samples. You can learn why in the lesson on the Mathematical Foundations of Monte Carlo Methods.

Noise is one of the major challenges with Monte Carlo path tracing. While noise may be tolerable in a still image, it becomes much more problematic in an animation sequence. Many recent CG animated feature films, such as *Finding Dory* or *Big Hero 6*, use a special technique called de-noising to address this issue. After rendering, noise can be partially removed using specialized image processing techniques.

How Do I Know That My Implementation Works? The Furnace Test

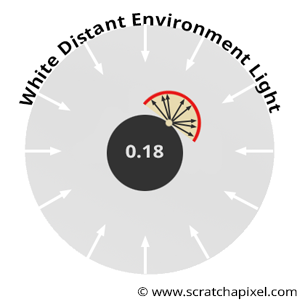
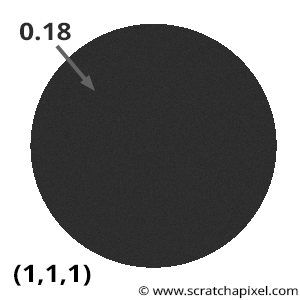
**Figure 5:** A sphere illuminated by a white spherical light source should have the color of the sphere’s albedo (0.18 in this example).

**Figure 6:** A sphere illuminated by a white spherical light source should have the color of the sphere’s albedo (0.18 in this example).

When implementing the technique described in this lesson, it’s important to verify that your implementation is correct. A simple way to test it is by rendering a gray sphere with an albedo of 0.18 (or 0.5; the exact value doesn’t matter). Imagine your gray sphere is enclosed by a larger white sphere emitting light. In code, this can be easily simulated by setting castRay() to return 1 when rays don’t intersect geometry and then rendering the gray sphere.

What result would you expect? Theory tells us that if the object is diffuse, then the albedo represents the proportion of light it reflects compared to what it receives. In this setup, each point on the gray sphere receives “white” light from every direction in the hemisphere above it. This light is reflected uniformly across the hemisphere, as is typical for diffuse surfaces. So, if a point receives “white” light from all directions and reflects 18% of it (assuming the sphere’s albedo is 0.18), each point on the sphere should have an intensity of exactly 0.18.

To test this, render a gray sphere with an albedo of 0.18 in a white environment. The rendered sphere should look like Figure 6, with a consistent intensity of 0.18 across its surface. If this isn’t the case, your code likely contains an error. When using Monte Carlo integration to render the image, each pixel may show slight variations in intensity, but as $N$ (number of samples) increases, the result should converge to 0.18. In computer graphics, this test is often called the furnace test.

The name comes from the property of a furnace in thermal equilibrium. When a furnace reaches equilibrium (when the energy received at a point equals the energy emitted), its interior appears uniform, and all geometric features seem to disappear.

Many things can go wrong when implementing global illumination. Common errors include failing to divide the illumination function by the PDF of the random variable, generating random variables with an incorrect distribution, or forgetting to multiply the light intensity by the cosine of the angle between the light direction and the surface normal.

Vec3f castRay(
    const Vec3f &orig, const Vec3f &dir,
    ...)
{
    if (trace(orig, dir, objects, isect)) {
        ...
        switch (isect.hitObject->type) {
            case kDiffuse:
            {
                ...
                Vec3f indirectLighting = 0;
#ifdef GI
                uint32_t N = 128; // (optional depth adjustment)
                Vec3f Nt, Nb;
                createCoordinateSystem(hitNormal, Nt, Nb);
                float pdf = 1 / (2 * M_PI);
                for (uint32_t n = 0; n < N; ++n) {
                    float r1 = distribution(generator);
                    float r2 = distribution(generator);
                    Vec3f sample = uniformSampleHemisphere(r1, r2);
                    Vec3f sampleWorld( 
                        sample.x * Nb.x + sample.y * hitNormal.x + sample.z * Nt.x,
                        sample.x * Nb.y + sample.y * hitNormal.y + sample.z * Nt.y,
                        sample.x * Nb.z + sample.y * hitNormal.z + sample.z * Nt.z);
                    // Don’t forget to divide by PDF and multiply by cos(theta)
                    indirectLighting += r1 * castRay(hitPoint + sampleWorld * options.bias,
                        sampleWorld, objects, lights, options, depth + 1) / pdf;
                }
                // Divide by N
                indirectLighting /= (float)N;
#endif
                hitColor = (directLighting + indirectLighting) * isect.hitObject->albedo / M_PI;
                break;
            }
            ...
        }
    }
    else {
        // Return white, as if a white spherical light illuminated the gray sphere
        hitColor = 1;
    }
    return hitColor;
}

int main(int argc, char **argv)
{
    ...
    Sphere *sph = new Sphere(Matrix44f::kIdentity, 1);
    sph->albedo = 0.18;
    objects.push_back(std::unique_ptr<Object>(sph));
    
    // Finally, render
    render(options, objects, lights);
    return 0;
}

Unbiased Path Tracing: What Does it Mean?

You may have heard the terms "biased" or "unbiased" path tracing. What do they mean? These concepts are introduced in the Mathematical Foundations of Monte Carlo Methods lesson. The estimator used in this lesson is:

$$\langle F^N \rangle = \dfrac{1}{N} \sum_{i=0}^{N-1} \dfrac{f(X_i)}{pdf(X_i)}.$$

This estimator is effective because it converges probabilistically to the exact solution of the integral, albeit slowly. As noted earlier, to reduce the noise in the image by half, four times as many samples are required. Other estimators can converge faster but introduce a small bias, meaning their results are slightly above or below the exact value. These are called "biased" estimators. When physical accuracy isn’t essential, biased estimators can be a better choice, as they produce images with less noise in a fraction of the time. For production renderers, achieving a balance between "accuracy" and speed is often crucial.

Environment and Image-Based Lighting

**Figure 7:** Direct illumination of a scene by a white distant environment light.

**Figure 8:** Direct illumination of a scene by a white distant environment light.

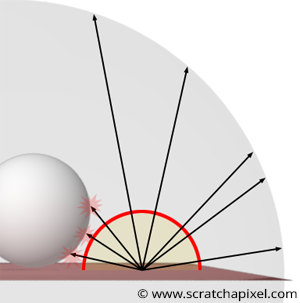
It’s possible to implement environment lighting with a simple code change. This simulates the illumination of objects by their surroundings—such as the sky or nearby structures—by surrounding objects with a spherical light source emitting light uniformly. Monte Carlo integration is then used to evaluate the light source’s contribution by casting $N$ rays distributed uniformly in the hemisphere above the shading normal.

Some rays may hit objects, blocking the light from reaching the shading point, as shown in Figure 8. When a ray doesn’t intersect geometry, it is assumed that the light source and shading point are mutually visible, meaning $P$ is illuminated by the light in that ray direction (Figure 8).

In this example, the spherical light source is assumed to be infinitely far from the shading points, so the square falloff rule doesn’t apply. These distant environment lights are commonly used to simulate ambient lighting from a distant environment.

Using this technique, we can calculate the amount of light reaching $P$ from the spherical light source, as shown on the left in the image below:

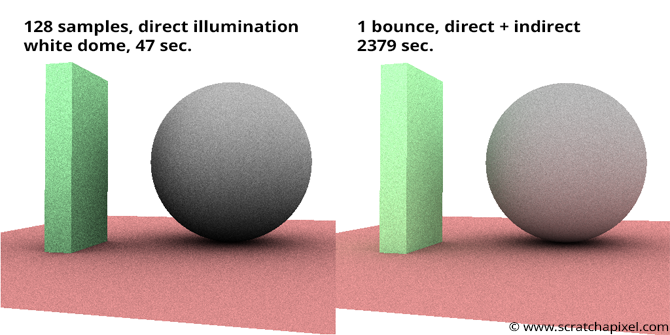
In this setup, Monte Carlo integration calculates direct illumination from the spherical light source. Global illumination can also be activated to account for light reflected by objects in the scene. Each time a ray cast from $P$ for direct illumination intersects an object, additional light reflection is considered. This approach becomes computationally expensive as the number of bounces increases. Adding direct and indirect illumination from a white environment light produces the image shown on the right.

Instead of using a constant color (e.g., white), you can "map" the spherical light with an image. When tracing a ray in a given direction, convert the Cartesian coordinates of the ray into spherical coordinates, then map these to image coordinates. These coordinates indicate the pixel in the image that illuminates $P$ along the ray’s direction. This technique, which uses real-world lighting information, is called image-based lighting. A lesson dedicated to this concept is available in the next section.

Why Is It Called Monte Carlo Path Tracing?

After all these explanations, the reason behind the name should now be clear. Monte Carlo refers to using Monte Carlo methods to solve global illumination, which is mathematically defined as an integral that captures all light illuminating $P$ from directions within the hemisphere above $P$. Path tracing refers to simulating light paths as rays bounce naturally from surface to surface or interact with materials like glass, water, or specular surfaces.

The technique described in this lesson is a form of light transport, also called unidirectional path tracing because it traces light paths in one direction—from the eye to the light sources. As you might guess, there’s another algorithm called bidirectional path tracing, which traces rays both from the eyes to objects and from light sources to objects, connecting the two to form complete light paths. This approach better simulates indirect specular reflections and caustics, and we’ll cover it in the next section.

Congratulations! You now have a solid understanding of rendering. In just a few lessons, you’ve explored light transport, Monte Carlo integration, BRDFs, and path tracing—some of the most challenging concepts in computer graphics.

Conclusion

Monte Carlo integration is straightforward for simulating global illumination in principle.
However, implementing it correctly requires a solid understanding of Monte Carlo theory, including PDFs, CDFs, estimators, and the inversion sampling method. Luckily, these topics are covered in-depth in our lessons on Monte Carlo methods (theory and practice).
Ray tracing is computationally expensive, and Monte Carlo path tracing, which uses many rays, becomes even more costly as sample size or bounce count increases. Acceleration techniques for ray tracing are essential and will be discussed in the next section.
Noise is a significant challenge in Monte Carlo path tracing, and noise reduction techniques will be explored in the following section.
Monte Carlo integration can also be used to simulate direct lighting from distant environment lights. Image-based lighting, based on this concept, will be covered in the next section.

More details on these topics await in the next section!

Reference

The Rendering Equation. Siggraph 1986, James T. Kajiya.

Global Illumination and Path Tracing