A Minimal Ray-Tracer

Ray-Box Intersection

Ray-Box Intersection

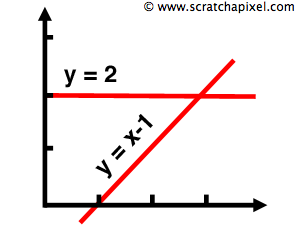
In this example, we consider a box aligned with the axes of our Cartesian coordinate system, referred to as an axis-aligned box or an axis-aligned bounding box (AABB). Boxes not aligned along the axis of a Cartesian coordinate system are known as oriented bounding boxes (OBB). The process to compute the intersection of a ray with an AABB is relatively straightforward. It's essential to recall that a straight line can be defined as:

In mathematics, the term \(m\) is known as the slope (or gradient) and determines the line's orientation, while \(b\) denotes the point where the line intersects the y-axis. If this 1D line is parallel to the x-axis, as illustrated in Figure 1 (with the line whose equation is \(y=2\)), then \(m\) equals 0. Similarly, a ray can be expressed as:

Here, \(O\) represents the origin of the ray, \(D\) its direction, and \(t\) can be any real value (negative, positive, or zero). Modifying \(t\) in this equation allows the definition of any point on the line defined by the ray's position and direction. This equation bears a resemblance to the line equation. In essence, they are equivalent: \(O\) corresponds to \(b\) and \(D\) to \(m\). To delineate an axis-aligned bounding volume, we use two points indicating the box's minimum and maximum extents (referred to as bounds in the code).

class Box3
{
public:
    Box3(const Vec3f &vmin, const Vec3f &vmax)
    {
        bounds[0] = vmin;
        bounds[1] = vmax;
    }
    Vec3f bounds[2];
};

The volume bounds define a set of lines parallel to each axis of the coordinate system, which we can also express using the line equation. Let's say we have a line defined by the equation:

Where \(B0_x\) is the x-component of the bounding box's minimum coordinates (that would be bounds[0].x in the code). To find where the ray intersects this line, we can write:

Which can be solved by reordering the terms:

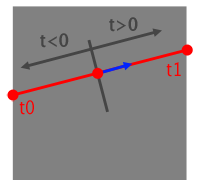
The x-component of the bounding volume's maximum extent can be used similarly to calculate the variable \(t_{1x}\). Note that when the values for \(t\) are negative, intersections are "behind" the ray (behind with respect to the ray's origin \(O\) and its direction \(D\)). Finally, if we apply the same technique to the y and z components, at the end of this process, we will have a set of six values indicating where the ray intersects the planes defined by the six faces of the box.

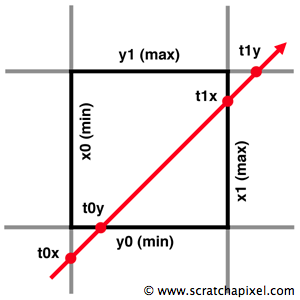
Note that if the ray is parallel to an axis, it won't intersect with the bounding volume plane for this axis (in this case, the line equation for the ray is reduced to the constant \(b\), and there's no solution to equation 1). The next step is to find which of these six values corresponds to an intersection of the ray with the box (if the ray intersects the box at all). So far, we have just found where the ray intersects the planes defined by each face of the box. We know this can be found using each of the calculated \(t\) values. By looking at Figure 2, the logic behind this test will become clear (we will just be considering the 2D case for this example). The ray first intersects the planes defined by the minimum extent of the box in two places: \(t_{0x}\) and \(t_{0y}\). However, intersecting these planes doesn't necessarily mean that these intersecting points lie on the cube (if they don't lie on the cube, the ray doesn't intersect the box). Mathematically, we can find which of these two points lies on the cube by comparing their values: for that, we need to choose the point whose \(t\) is the biggest. In pseudo-code, we can write:

t0x = (B0x - Ox) / Dx;
t0y = (B0y - Oy) / Dy;
tmin = (t0x > t0y) ? t0x : t0y;

The process to find the second point where the ray intersects the box is similar; however, in that case, we will use the \(t\) values calculated using the planes defined by the maximum extent of the box and select the point whose \(t\) is the smallest:

t1x = (B1x - Ox) / Dx;
t1y = (B1y - Oy) / Dy;
tmax = (t1x < t1y) ? t1x : t1y;

The ray doesn't necessarily intersect the box. Figure 3 illustrates several scenarios where the ray misses the cube. By comparing the \(t\) values, we can determine these cases. As depicted in the figure, the ray misses the box when \(t_{0x}\) is greater than \(t_{1y}\) or when \(t_{0y}\) is greater than \(t_{1x}\). Let's incorporate this test into our code:

if (t0x > t1y || t0y > t1x) return false;

We can extend this technique to the 3D case by computing \(t\) values for the z-component and comparing them to the \(t\) values calculated for the x and y components:

t0z = (B0z - Oz) / Dz; 
t1z = (B1z - Oz) / Dz; 
if (tmin > t1z || t0z > tmax) 
    return false; 
if (t0z > tmin) tmin = t0z; 
if (t1z < tmax) tmax = t1z;

Below is a complete implementation of the method in C++. The variables min and max represent the minimum and maximum extents (coordinates) of the bounding box:

bool intersect(const Ray &r) { 
    float tmin = (min.x - r.orig.x) / r.dir.x; 
    float tmax = (max.x - r.orig.x) / r.dir.x; 

    if (tmin > tmax) swap(tmin, tmax); 

    float tymin = (min.y - r.orig.y) / r.dir.y; 
    float tymax = (max.y - r.orig.y) / r.dir.y; 

    if (tymin > tymax) swap(tymin, tymax); 

    if ((tmin > tymax) || (tymin > tmax)) 
        return false; 

    if (tymin > tmin) tmin = tymin; 
    if (tymax < tmax) tmax = tymax; 

    float tzmin = (min.z - r.orig.z) / r.dir.z; 
    float tzmax = (max.z - r.orig.z) / r.dir.z; 

    if (tzmin > tzmax) swap(tzmin, tzmax); 

    if ((tmin > tzmax) || (tzmin > tmax)) 
        return false; 

    if (tzmin > tmin) tmin = tzmin; 
    if (tzmax < tmax) tmax = tzmax; 

    return true; 
}

Note that depending on the ray's direction, tmin might be greater than tmax. Given that all the logic behind our tests relies on \(t_0\) being smaller than \(t_1\), we need to swap the values if \(t_1\) is smaller than \(t_0\).

Optimizing the Code

There are several improvements we can make to this code to enhance its performance and robustness. First, we can replace the swap operation with the following condition to account for the ray's direction:

if (ray.dir.x >= 0) { 
    tmin = (min.x - r.orig.x) / ray.dir.x; 
    tmax = (max.x - r.orig.x) / ray.dir.x; 
} else { 
    tmin = (max.x - r.orig.x) / ray.dir.x; 
    tmax = (min.x - r.orig.x) / ray.dir.x; 
}

This adjustment ensures that the algorithm efficiently handles rays in different directions and optimizes the calculation of \(t_{min}\) and \(t_{max}\) by eliminating unnecessary swaps.

However, this code needs fixing. When the value for the ray's x, y, or z component is 0, it leads to division by zero. The compiler should handle this gracefully and return +INF in such cases, which might not seem problematic at first glance. The issue arises because compilers do not differentiate between 0 and -0 (they consider -0 == 0 and will return true). Therefore, if any of the ray direction's components is -0, the values for tmin/tmax will be set to +INF and -INF, respectively, rather than -INF and +INF. This misinterpretation causes the algorithm to execute the wrong block of the if-statement (the condition should evaluate to false for a negative value, not true). Consequently, it may fail to detect an intersection. To rectify this, we can replace the ray direction with the inverse of the ray direction:

Vec3f invdir = 1 / ray.dir; 
if (invdir.x >= 0) { 
    tmin = (min.x - r.orig.x) * invdir.x; 
    tmax = (max.x - r.orig.x) * invdir.x; 
} 
else { 
    tmin = (max.x - r.orig.x) * invdir.x; 
    tmax = (min.x - r.orig.x) * invdir.x; 
}

When the ray direction is -0, the inverse value of the direction's component will be -INF, making the test if (invdir.x >= 0) correctly return false as intended. If testing the intersection of the ray against many boxes, time can be saved by pre-computing the inverse direction of the ray in the ray's constructor and re-using it in the intersect function. We can also pre-compute the sign of the ray direction, allowing us to write the method in a much more compact form. Here is the final version of the ray-box intersection method:

class Ray
{
public:
    Ray(const Vec3f &orig, const Vec3f &dir) : orig(orig), dir(dir)
    {
        invdir = 1 / dir;
        sign[0] = (invdir.x < 0);
        sign[1] = (invdir.y < 0);
        sign[2] = (invdir.z < 0);
    }
    Vec3<T> orig, dir;       // Ray origin and direction
    Vec3<T> invdir;
    int sign[3];
};
 
bool intersect(const Ray &r) const
{
    float tmin, tmax, tymin, tymax, tzmin, tzmax;
    
    tmin = (bounds[r.sign[0]].x - r.orig.x) * r.invdir.x;
    tmax = (bounds[1-r.sign[0]].x - r.orig.x) * r.invdir.x;
    tymin = (bounds[r.sign[1]].y - r.orig.y) * r.invdir.y;
    tymax = (bounds[1-r.sign[1]].y - r.orig.y) * r.invdir.y;
    
    if ((tmin > tymax) || (tymin > tmax))
        return false;

    if (tymin > tmin)
        tmin = tymin;
    if (tymax < tmax)
        tmax = tymax;
    
    tzmin = (bounds[r.sign[2]].z - r.orig.z) * r.invdir.z;
    tzmax = (bounds[1-r.sign[2]].z - r.orig.z) * r.invdir.z;
    
    if ((tmin > tzmax) || (tzmin > tmax))
        return false;

    if (tzmin > tmin)
        tmin = tzmin;
    if (tzmax < tmax)
        tmax = tzmax;

    return true;
}

The optimized version runs on our machine approximately 1.5 times faster than the first version, though the exact speedup depends on the compiler.

The code from this lesson returns intersections with the box both in front of and behind the ray's origin. For instance, if the ray's origin is inside the box (as shown in the adjacent image), there will be two intersections: one in front of the ray and one behind. We determine that an intersection is "behind" the ray's origin if \(t\) is negative. Conversely, when \(t\) is positive, the intersection is in front of the ray's origin, relative to the ray's direction.

For a complete example, refer to the file raybox.cpp, which is available on the GitHub repository.

Reference

An Efficient and Robust Ray–Box Intersection Algorithm by Amy Williams et al., 2004.