Displaying Images to the Screen
Reading time: 13 mins.In the previous lesson, we learned about colors and the concept color space. The ultimate goal of making images though is to display them in some ways so that people can look at them. Which requires that we not only learn about encoding color values as we did in the previous chapter, but that we also learn how these colors are interpreted, decoded or manipulated by display devices as well as how the human vision system which is last in the chain, responds to visual stimuli. In this lesson, we will look at three aspects in this chain which can influence the quality of the images we are looking at on a computer screen: the human eye itself and the way it reacts to brightness, the screen technology and finally the way we encode pixel values in an image file (second chapter).
Linear Color Space
We mentioned in the previous lesson that the XYZ and RGB color spaces were linear. What does it mean? A color space is linear if when you multiply a color expressed in this system by a certain factor (say three) the brightness or luminance of this color is also multiplied by the same factor (three in our example). Linearity in that context refers to the relationship between values and the brightness of the resulting color. In computer graphics, the color values that a renderer is dealing with are always expressed in a linear color space. Things would be simple if linearity was preserved everywhere, however in reality we need to take into consideration two factors: the human vision (again) and display devices such as computer screens which unfortunately are non-linear. Let's start with human vision.
Human Vision: Brightness Adaptation
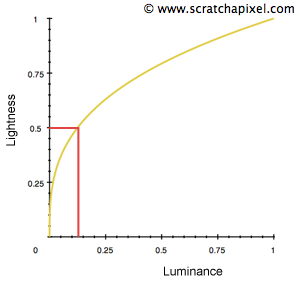
We already learned quite a few things in the previous lesson on the physiology of color perception such as the trichromatic color vision, scotopic (vision in low light conditions) and photopic vision (vision in normal light conditions), the luminosity function that describes the visual sensitivity of the human eye to light of different wavelengths, etc. One other important properties of human vision that we haven't talked about yet is the way it reacts to brightness. With very little light we are already capable of discerning things. Using a candle is enough to start discerning things in a room although it is far less brighter than the sun. Overall the range of light intensities that the human can adapt to is very large and is roughly \({1}\) to \({10^{10}}\). However we can not perceive this range of intensities at once. The light of a candle is unlikely to make any difference to the perceived brightness of a scene watched on a sunny day. The way our eye manages to deal with such a large range of illumination levels is by changing its sensitivity to the overall brightness of a scene. This capacity of the eye to adapt very quickly to light intensity levels (mainly through dilation and contraction of the iris) is known as brightness adaptation. Furthermore the response to light-intensity levels is also non linear. It simply means that the eyes can locally adapt to the various illumination levels of a scene and perceive darker regions much brighter than they truly are in comparison to the bright parts of the scene (human vision is more sensitive to small brightness variations in dark regions than in bright regions). A source having a luminance only 18% of a reference luminance for example appears about half as bright. The non-linear perceptual response of the human vision to luminance is called lightness. Generally, it is admitted that this response (perceptual brightness vs real luminance) is roughly a cube-root function (Figure 1):
$$lightness = luminance^{{1 \over 3}}$$We should therefore keep in mind that the way we perceive the brightness levels of an image displayed on a screen is influenced by the the amount of light surrounding the screen (because of the brightness adaptation phenomenon) and that the relationship between the perceived brightness of a color (lightness) and the actual luminance of this color is linked by a nonlinear relationship.
Computer Displays: Gamma Correction
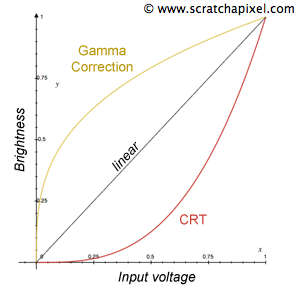
Computer screens too have their own properties which we need to be aware of when we want to display images in a way that is controllable (that is being sure that once the image is created, different viewers can see the same colors and brightness levels independently from the display devices which is being used). In the early ages of computers, most monitors were using CRTs (cathode ray tube). The problem with these screens was that the energy or voltage used to control the brightness of a point on the screen and the brightness of that point was not linear. The relationship voltage and pixel brightness was not linear. Plotting the voltage used vs the brightness produced on the screen gave the curve from Figure 2. This nonlinear relationship between brightness and voltage can be represented using the following equation:
$$brightness = voltage^{\gamma}$$where the exponent parameter of this power function called \(\gamma\) (the Greek letter gamma) is somewhere between 2.35 and 2.55. What is noticeable about the curve from Figure 2 is that it looks like the opposite of the curve from Figure 1 but that is only a coincidence. This property of the CRT monitors was a serious issue as it modifies the levels of the displayed images, making the lower values notably darker than they actually should. The solution to this problem was to apply an inverse gamma which was called a gamma correction.
$$brightness = image^{{1 \over \gamma}} \cdot voltage^{\gamma} \rightarrow \text{linear curve}$$This gamma correction was usually applied by cameras. In the old times, computer generated images which as we mentioned already have all their colors produced in linear color space, had also to be saved or displayed with a gamma correction to compensate for the monitor's gamma. Today though CRT screens are replaced by LCDs, LED or plasma monitors which are linear so in theory, we shouldn't have to care so much about this CRT gamma and gamma correction anymore. However in practice, computer displays still use a gamma correction independently from the technology they use (even though their curve function, the ratio between the input-output values, is linear). And we will now explain why.
Gamma Encoding
At the beginning of this chapter we talked about how human vision doesn't react linearly to the brightness levels of a picture. Under common illumination conditions, our vision follows an approximate gamma function (which we showed the shape of in Figure 1). However, computer programs don't know anything about human physiology and save the pixel values of an image in linear space. If you think of an image format in which the value 100 represents white, then from the computer's point of view, a pixel whose value is 20 is twice as bright as a pixel whose value is 10. And for this computer, jumps of 10 in values (starting from 0 up to 100) correspond to regular increases of brightness. Our vision system however responds differently to this image. It will see much bigger jumps in darker areas while hardly perceiving any brightness variations in the bright areas (eyes have an extremely good color and tone discrimination capability in the dark values).

You may already know that we generally use 8 bits per channel per pixel to save RGB images. And with 8 bits you can only represent numbers going from 0 to 255\. Since we can use 255 for each primary color (red, green and blue) this represents a total of roughly 1.6 million possible color combinations (256*256*256). Now as we mentioned before, the computer only knows about numbers and the natural way of encoding brightness values is to say that 255 (since it is the maximum value we can represent with 8 bits) represents white, 0 is black and 128 defines mid-gray. In that system, there is a linear relationship between the value used (from 0 to 255) and the brightness level they technically represent (the gray scale). However we know that the human eye is more sensitive to change in darker regions of the image than it is to changes in brighter regions. Therefore, we would do a much better use of these 8 bits if grays values lower than 50% (which is an arbitrary number just to establish a limit between dark and bright values) could be saved in the file with greater precision in order to better capture the changes in values between low intensities to which the eyes is very sensitive.

If we use more bits to encode dark values then it means that we are left with less bits to encode the bright ones but this doesn't matter much since we don't perceive variations between bright values as well as we do between dark values. How shall we achieve this using only 8 bits? The answer is simple and relies on using a gamma trick again. We apply a gamma whose exponent is usually around 1/2.2 to the pixel values that come out from the camera's CCD or from a 3D renderer. These values are usually expressed in a floating-point format (float in C++). The gamma curve looks like the one showed in Figure 4. Once the gamma encoding is applied, we then convert these values to a type byte (8 bits) before saving the data to an image file. As you can see in Figure 4, a value of 0.5 (representing mid-gray in linear space assuming a floating-point value of 1 is white) maps to a byte value greater than 128 once the gamma encoding is applied. Now we are left with one last problem. It is important to understand that the goal of this trick is only to have more room to encode the lower values of an image. We still want to display the image on the screen in linear space. Now that we have encoded a gamma to the image's data we need to remove it when we display the image back onto the screen. Which we naturally do by applying to the screen a gamma correction of 2.2 (the inverse of the encoding gamma we have to the image data). How did we come with a value of 2.2 rather than 2.6 is explained further down.
In conclusion, what you need to remember is that old CRT monitors were non linear. The relationship between the pixel value and the brightness on the screen follows a power curve which exponent is roughly around 1/2.35 to 1/2.5. To compensate we had to apply a gamma a 2.35 to 2.5 gamma correction to the image. Nowadays we don't use CRT monitors anymore; they are replaced by display technologies (LCD, LED) which are linear. However (and this is the reason the sRGB color space was invented) we still decided to apply a 1/2.2 gamma encoding to the image data to maximize the number of lower values we could encode in 8 bits RGB images. To display these images linearly, a 2.2 gamma correction is applied to the screen (no matter which device technology you use which is likely to be these days a screen which can display pixel values linearly). End of story. The main misconception regarding this whole 2.2 gamma topic is that, it is necessary to correct the non-linearity of your screen. If it used to be true in the old days, it is not true today as displays are now linear. Screens only apply a 2.2 gamma correction to "remove" the gamma encoding applied to 8 bits RGB images.
This gamma encoding is only necessary for image formats saving data using 8 bits per pixel per channel. Gamma encoding is not necessary for file formats saving pixel values using 16 (half float) or 32 bits (float) per pixel per channel (you will find more details on this topic in the next chapter) as they provide enough numerical precision to store all the nuances of tones we need. Even though we could use these formats instead, they use more disk space and more bandwidth when transferred on the internet, and for these reasons, 8 bits file formats such as JPEG, PNG, TGA, etc. are still the standard for storing images (this apply to video images as well). If you work in the graphics industry though, it is likely that you already use 16 or 32 bits file format such as TIFF, OpenEXR, HDR, RAW, in which case it is important that you don't forget to remove the 2.2 screen gamma correction in order to watch these images in linear.
The sRGB Color Space
The sRGB color space was an attempt from Microsoft and HP (in 1996 ) to come up with a way of standardising the encoding of pixel values in 8 bits RGB images. The format enforces the use of a gamma 1/2.2 (technically the exponent is actually 2.4). Encoding the gamma was originally motivated by the necessity of compensating for the CRT non-linearity but is now justified for the reasons we have mentioned above (we can encode more data in the lower tones). In a future version of this document we will provide more information on this color space (the technical specifications of the format are are easy to find on the web). We have only mention it here because most of the images you are looking or downloading from the web are probably encoded using this format. Remember though that 3D engines work in linear color space so if you intend to use an sRGB image as a texture source or if you pick up colors from the image you will need to "linearise" the image first (aka apply a 2.2 gamma correction to image).