How Does Matrix Work: Part 2
Reading time: 6 mins.Understanding the Link Between Matrices and the Cartesian Coordinate System
Consider a scenario where you have a point \(P_x\) with coordinates (1, 0, 0) and you wish to rotate it around the z-axis by 10 degrees in a clockwise direction. How would the coordinates of this point change? By applying our knowledge of rotation matrices, we recognize that the new coordinates can be determined through basic trigonometry. The x-coordinate of the newly rotated point \(P_x\) can be calculated using cos(-10), while the y-coordinate is obtained using sin(-10) (noting that trigonometric functions in C++ require angles to be in radians). Similarly, if we rotate a point \(P_y\) with coordinates (0, 1, 0) by the same angle, the resulting x-coordinate will be -sin(-10), and the y-coordinate will be cos(-10). It's interesting to note that the trigonometric functions used to calculate the new coordinates of \(P_x\) are mirrored in the first row of the rotation matrix \(R_Z\), which is used for rotating points around the z-axis. A similar pattern is observed in the matrix's second row, reflecting the trigonometric calculations for the rotated \(P_y\) coordinates:
$$ \begin{array}{ll} P_x^x = \cos(\theta) & P_x^y = \sin(\theta) \\ P_y^x = -\sin(\theta) & P_y^y = \cos(\theta) \end{array} $$As we proceed to rotate the axes around the z-vector, the computation of new coordinates for \(P_x\) aligns with the matrix's first row, and \(P_y\)'s coordinates align with the second row. If this process is applied to a point \(P_z\) considering the rotation matrices \(R_X\) or \(R_Y\), it becomes evident that \(P_z\)'s new coordinates are derived from the third row of the chosen matrix, depending on the axis around which \(P_z\) is rotated.
The essence of matrices lies in the fact that each matrix row signifies an axis (or basis) of a coordinate system. This understanding is crucial as it lays the groundwork for later learning about the creation of matrices to transform points and vectors from one coordinate system to another (change of basis). This is accomplished by substituting the matrix rows with the coordinates of each new coordinate system's axis into which you aim to transform your vectors or points:
$$ \begin{bmatrix} \color{red}{c_{00}} & \color{red}{c_{01}} & \color{red}{c_{02}} \\ \color{green}{c_{10}} & \color{green}{c_{11}} & \color{green}{c_{12}} \\ \color{blue}{c_{20}} & \color{blue}{c_{21}} & \color{blue}{c_{22}} \\ \end{bmatrix} \begin{array}{l} \rightarrow \quad \color{red} {x-axis} \\ \rightarrow \quad \color{green} {y-axis} \\ \rightarrow \quad \color{blue} {z-axis} \\ \end{array} $$This technique, a staple in computer graphics, will be explored in upcoming chapters. The mystery around matrices dissipates when you grasp that they essentially serve to store the coordinates of a coordinate system, with each matrix row representing one of the system's axes, or what is sometimes referred to as an orientation matrix.
The discussion above pertains to matrices in row-major order, where each row of the matrix corresponds to an axis of the Cartesian coordinate system. It's essential to highlight that if you're working with column-major order matrices, a different approach is necessary. In column-major order matrices, each column, rather than each row, aligns with one of the Cartesian coordinate system's axes (x, y, and z, respectively). This distinction is crucial for accurately transforming points and vectors between coordinate systems. Therefore, when utilizing column-major order matrices for transformations, you must consider that the orientation and basis vectors of the coordinate system are represented by the columns of the matrix, not the rows. This adjustment ensures that the matrix accurately reflects the transformation in the intended coordinate system.
In 4x4 matrices, the translation components are specifically allocated, differing in placement depending on the matrix's order. For row-major order matrices, translation values are positioned in the matrix's fourth row, precisely at m[3][0], m[3][1], and m[3][2] for the x, y, and z translation values, respectively. This placement facilitates the integration of translation with rotation and scaling operations within a single matrix, streamlining transformations in three-dimensional space. Conversely, when dealing with column-major order matrices, the translation values shift to the fourth column. This difference in storage location underscores the importance of understanding the matrix order being used, as it directly influences how transformations are applied and interpreted.
Orthogonal Matrices and Their Role in Linear Algebra
Orthogonal matrices, a central topic discussed in this and the preceding chapter, are square matrices with real entries where both columns and rows consist of orthogonal unit vectors. These matrices, particularly rotation matrices or those derived from multiplying several rotation matrices, inherently represent the axes of a Cartesian coordinate system with unit length axes. This characteristic arises because their row elements are derived from sine and cosine functions, which calculate points on the unit circle, mirroring a Cartesian coordinate system initially aligned with the world coordinate system (where the identity matrix's rows signify the world coordinate system's axes) that has been rotated around a specific or arbitrary axis. A key attribute of orthogonal matrices, highly valuable in Computer Graphics, is their property where the transpose of an orthogonal matrix equals its inverse. Represented mathematically as \(Q^T=Q^{-1}\), it implies \(QQ^T=I\), with \(I\) being the identity matrix. This property underscores the ease of reversing transformations by simply transposing the orthogonal matrix, a concept elaborated upon in the chapter on Matrix Operations.
Affine Transformations in Computer Graphics
The term affine transformations frequently substitutes matrix transformation discussions, offering a more precise designation for the transformations achieved through the matrices outlined previously. Affine transformations are defined by their linearity and the preservation of points, straight lines, and planes. Common transformations like translation, rotation, and shearing fall under affine transformations, as do their combinations. This sets the stage for exploring projective transformations in Computer Graphics, which include perspective projection and are characterized by their alteration of line parallelism, an aspect further explored in discussions on perspective and orthographic projection matrices in the Foundation of 3D Rendering section.
Summary and Visualization
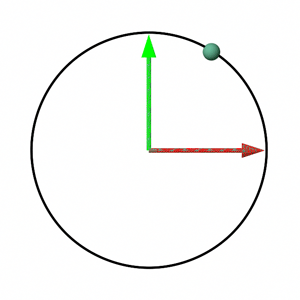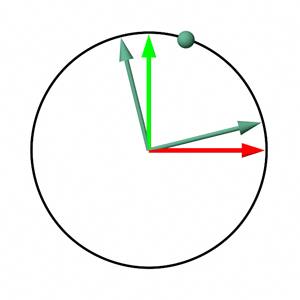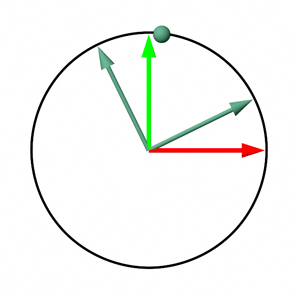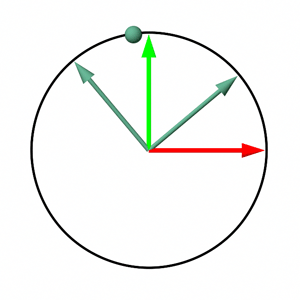
The chapters provide not only the methodology for constructing rotation matrices but also a conceptual framework for understanding matrices. Each matrix row is conceptualized as an axis within a Cartesian coordinate system, with the matrix as a whole representing the transformation (rotation, scale, translation) applied to points when multiplied. This framework suggests that points defined within a coordinate system (A) and attached to a local coordinate system (B) or matrix, will retain their coordinates relative to B even as B undergoes transformations. However, their coordinates relative to A will change, illustrating the transformation impact. This principle is visually depicted in figure 6, showing how a point's coordinates evolve relative to the world coordinate system (and remain constant relative to the rotation matrix-defined coordinate system) through rotation.
Key takeaways include the derivation of basic rotation matrices, the significance of matrix multiplication order, and the conceptualization of a matrix as a local Cartesian system (orientation matrix). This understanding is further expanded upon in the chapter Creating an Orientation Matrix or Local Coordinate System, emphasizing the foundational role of matrices in graphical transformations.