The Perspective and Orthographic Projection Matrix

The Orthographic Projection Matrix

What Do I Need Orthographic Projection For?

The orthographic projection (sometimes also referred to as oblique projection) is simpler compared to other projection types, making it an excellent subject for understanding how the perspective projection matrix operates. You might question the relevance of orthographic projections in modern applications, given the prevalent pursuit of photorealism in films and games, typically achieved through perspective projection. However, orthographic or parallel projection has its unique applications and benefits. For instance, video games like The Sims or Sim City have utilized this projection method to achieve a distinct visual style that, in certain contexts, is preferred over the more conventional perspective projection. Moreover, orthographic projection is instrumental in rendering shadow maps or producing orthographic views of a 3D model for practical purposes. An architect, for example, might need to generate blueprints from a 3D model of a house or building designed in CAD software.

In this chapter, we will explore how to construct a matrix that projects a point from camera space onto the image plane of an orthographic camera.

The aim of the orthographic projection matrix is to remap all coordinates within a specific 3D space bounding box to the canonical viewing volume—a concept introduced in Chapter 2. Imagine this original box as a bounding box encompassing all objects within your scene. By iterating over each object in the scene, calculating their bounding boxes, and adjusting the dimensions of the global bounding box to include all these volumes, you establish the scene's bounding box. The orthographic matrix then aims to remap this box to a canonical view volume, defined by minimum and maximum extents of (-1, -1, -1) and (1, 1, 1) (or (-1, -1, 0) and (1, 1, 1), depending on the convention used). Essentially, the x- and y-coordinates of the projected point are mapped from their original range to [-1,1], with the z-coordinate adjusted to fall within [-1,1] (or [0,1]). It's noteworthy that both bounding boxes—the scene's and the canonical view volume—are AABBs (axis-aligned bounding boxes), which significantly simplifies the remapping process.

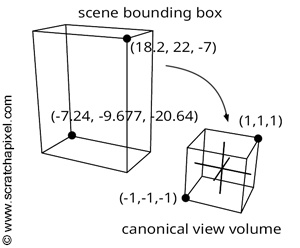
Once we have computed the scene bounding box, we need to project the minimum and maximum extents of this bounding box onto the image plane of the camera. In the case of an orthographic projection (or parallel projection), this task is straightforward. The x- and y-coordinates of any point expressed in camera space and the x- and y-coordinates of the same points projected onto the image plane remain identical. It may be necessary to adjust the projection of the bounding box's minimum and maximum extents onto the screen to ensure the screen window is either square or maintains the same aspect ratio as the image (see the code of the test program below for implementation details). Also, remember that the canvas or screen is centered around the origin of the screen coordinate system (Figure 2).

We will refer to these screen coordinates as l, r, t, and b, which stand for left, right, top, and bottom, respectively.

Now, we need to remap the left and right screen coordinates (l, r) to -1 and 1, and apply the same remapping to the top and bottom coordinates (t, b). Let's explore how this can be achieved. Assuming x is any point within the range \([l,r]\), we can state:

Subtracting l from all terms yields:

To normalize the right-hand term to 1 instead of \(r\), we divide everything by \(r - l\), resulting in:

Multiplying the entire equation by 2 (the reason for this will become clear shortly):

Subtracting 1 from all terms gives us:

Now, the middle term falls within the range \([-1,1]\), successfully remapping it. To further develop this formula:

Simplifying:

Rearranging:

This yields the transformation formula for x:

To represent this transformation in matrix form (as you may recall from Chapter 3):

The process for the y-coordinate is the same. You just need to replace \(r\) and \(l\) with \(t\) and \(b\) (top and bottom). The matrix becomes:

And finally, to complete our orthographic projection matrix, we need to remap the z-coordinates from -1 to 1. We will use the same principle to find a formula for \(z\). We start with the following condition:

Don't forget that because we use a right-hand coordinate system, the z-coordinates of all points visible to the camera are negative, which is why we use \(-z\) instead of \(z\). We set the term on the left to 0:

Then, divide everything by \(f-n\) to normalize the term on the right:

Multiply all the terms by two:

Subtract one:

We can rewrite it as:

Developing the terms, we get:

Rearranging the terms gives:

Let's add these two terms to the matrix:

Remember that OpenGL uses a column-major convention to encode matrices, whereas Scratchapixel uses a row-major notation. To transition from one notation to the other, you need to transpose the matrix. Below is the final OpenGL orthographic matrix as typically seen in textbooks:

Test Program

As usual, we will test the matrix with a simple program. We will reuse the same code as the one we used to test both the simple and the OpenGL perspective projection matrix. We have replaced the glFrustum function with a function called glOrtho, which, as the name suggests, is used to set an OpenGL orthographic matrix. The screen coordinates (the l, r, t, and b parameters of the function) are computed as follows (lines 63-83): the scene's bounding box is calculated by iterating over all vertices in the scene and extending the minimum and maximum extent variables accordingly. The bounding box's minimum and maximum extents are then transformed from world to camera space. From the two resulting points in camera space, we find the maximum dimension in both x and y. We finally set the screen coordinates to the maximum of these two values. This ensures that the screen coordinates form a square (you may need to multiply the left and right coordinates by the image aspect ratio if it is different from 1) and that the screen or canvas itself is centered around the screen space coordinate system origin.

The rest of the code follows as usual. We loop over the vertices in the scene. Vertices are transformed from world to camera space and then projected onto the screen using the OpenGL orthographic projection matrix.

#include <cstdio>
#include <cstdlib>
#include <fstream>
#include <limits>
#include "geometry.h"
#include "vertexdata.h"

// Set the OpenGL orthographic projection matrix
void glOrtho(
    const float &b, const float &t, const float &l, const float &r,
    const float &n, const float &f,
    Matrix44f &M)
{
    // Set the OpenGL orthographic projection matrix
    M[0][0] = 2 / (r - l);
    M[0][1] = 0;
    M[0][2] = 0;
    M[0][3] = 0;

    M[1][0] = 0;
    M[1][1] = 2 / (t - b);
    M[1][2] = 0;
    M[1][3] = 0;

    M[2][0] = 0;
    M[2][1] = 0;
    M[2][2] = -2 / (f - n);
    M[2][3] = 0;

    M[3][0] = -(r + l) / (r - l);
    M[3][1] = -(t + b) / (t - b);
    M[3][2] = -(f + n) / (f - n);
    M[3][3] = 1;
}

void multPointMatrix(const Vec3f &in, Vec3f &out, const Matrix44f &M)
{
    // Multiply point by projection matrix
    out.x = in.x * M[0][0] + in.y * M[1][0] + in.z * M[2][0] + M[3][0];
    out.y = in.x * M[0][1] + in.y * M[1][1] + in.z * M[2][1] + M[3][1];
    out.z = in.x * M[0][2] + in.y * M[1][2] + in.z * M[2][2] + M[3][2];
    float w = in.x * M[0][3] + in.y * M[1][3] + in.z * M[2][3] + M[3][3];

    // Normalize if w is different than 1 (convert from homogeneous to Cartesian coordinates)
    if (w != 1) {
        out.x /= w;
        out.y /= w;
        out.z /= w;
    }
}

int main(int argc, char **argv)
{
    uint32_t imageWidth = 512, imageHeight = 512;
    Matrix44f M

proj;
    Matrix44f worldToCamera = {0.95424, 0.20371, -0.218924, 0, 0, 0.732087, 0.681211, 0, 0.299041, -0.650039, 0.698587, 0, -0.553677, -3.920548, -62.68137, 1};

    float near = 0.1;
    float far = 100;
    float imageAspectRatio = imageWidth / (float)imageHeight; // 1 if the image is square

    // Compute the scene bounding box
    const float kInfinity = std::numeric_limits<float>::max();
    Vec3f minWorld(kInfinity), maxWorld(-kInfinity);
    for (uint32_t i = 0; i < numVertices; ++i) {
        if (vertices[i].x < minWorld.x) minWorld.x = vertices[i].x;
        if (vertices[i].y < minWorld.y) minWorld.y = vertices[i].y;
        if (vertices[i].z < minWorld.z) minWorld.z = vertices[i].z;
        if (vertices[i].x > maxWorld.x) maxWorld.x = vertices[i].x;
        if (vertices[i].y > maxWorld.y) maxWorld.y = vertices[i].y;
        if (vertices[i].z > maxWorld.z) maxWorld.z = vertices[i].z;
    }

    Vec3f minCamera, maxCamera;
    multPointMatrix(minWorld, minCamera, worldToCamera);
    multPointMatrix(maxWorld, maxCamera, worldToCamera);

    float maxx = std::max(fabs(minCamera.x), fabs(maxCamera.x));
    float maxy = std::max(fabs(minCamera.y), fabs(maxCamera.y));
    float max = std::max(maxx, maxy);
    float r = max * imageAspectRatio, t = max;
    float l = -r, b = -t;

    glOrtho(b, t, l, r, near, far, Mproj);
    unsigned char *buffer = new unsigned char[imageWidth * imageHeight];
    memset(buffer, 0x0, imageWidth * imageHeight);
    for (uint32_t i = 0; i < numVertices; ++i) {
        Vec3f vertCamera, projectedVert;
        multPointMatrix(vertices[i], vertCamera, worldToCamera);
        multPointMatrix(vertCamera, projectedVert, Mproj);
        if (projectedVert.x < -imageAspectRatio || projectedVert.x > imageAspectRatio || projectedVert.y < -1 || projectedVert.y > 1) continue;
        // Convert to raster space and mark the vertex position in the image with a simple dot
        uint32_t x = std::min(imageWidth - 1, (uint32_t)((projectedVert.x + 1) * 0.5 * imageWidth));
        uint32_t y = std::min(imageHeight - 1, (uint32_t)((1 - (projectedVert.y + 1) * 0.5) * imageHeight));
        buffer[y * imageWidth + x] = 255;
    }
    // Export to image
    std::ofstream ofs;
    ofs.open("./out.ppm");
    ofs << "P5\n" << imageWidth << " " << imageHeight << "\n255\n";
    ofs.write((char *)buffer, imageWidth * imageHeight);
    ofs.close();
    delete[] buffer;

    return 0;
}

As usual, we compare the result of our program with a render of the same geometry using the same camera and render settings. Overlaying the program's output on the reference render confirms that the program produces a matching result.