Row Major vs Column Major Vectors and Matrices
Reading time: 28 mins.Earlier in this lesson, we explained that vectors (or points) could be represented as [1x3] matrices (one row, three columns) or as [3x1] matrices (three rows, one column). Both forms are technically valid, and the choice between them is merely a matter of convention.
-
Vector represented as a [1x3] matrix:
$$V = \begin{bmatrix} x & y & z \end{bmatrix}$$ -
Vector represented as a [3x1] matrix:
$$V = \begin{bmatrix} x \\ y \\ z \end{bmatrix}$$
In the [1x3] matrix representation, the vector or point is in row-major order, meaning it is written as a row of three numbers. Conversely, in the [3x1] matrix representation, points or vectors are in column-major order, with the three coordinates of the vector or point written vertically as a column.
We use matrix representation for points and vectors to facilitate multiplication by [3x3] transformation matrices. For simplicity, we focus on [3x3] matrices rather than [4x4] matrices. Matrix multiplication is possible only when the number of columns in the left matrix matches the number of rows in the right matrix. Hence, a [1x3] matrix can be multiplied by a [3x3] matrix, but a [3x1] matrix cannot directly multiply a [3x3] matrix. This principle is demonstrated below, where the inner dimensions that match allow for valid multiplication (highlighted in green), resulting in a transformed point in the form of a [1x3] matrix:
$$ [1 \times \textcolor{green}{3}] \times [\textcolor{green}{3} \times 3] = \begin{bmatrix} x & y & z \end{bmatrix} \times \begin{bmatrix} c_{00} & c_{01} & c_{02} \\ c_{10} & c_{11} & c_{12} \\ c_{20} & c_{21} & c_{22} \end{bmatrix} = \begin{bmatrix} x' & y' & z' \end{bmatrix} $$However, when the inner dimensions do not match (highlighted in red), multiplication is not feasible:
$$ [3 \times \textcolor{red}{1}]*[\textcolor{red}{3} \times 3] \rightarrow \begin{bmatrix} x\\ y\\z \end{bmatrix} * \begin{bmatrix} c_{00}&c_{01}&{c_{02}}\\ c_{10}&c_{11}&{c_{12}}\\ c_{20}&c_{21}&{c_{22}} \end{bmatrix} $$To resolve this, instead of trying to multiply the vector or point by the matrix, we multiply the matrix by the vector, placing the point or vector to the right in the multiplication:
$$ [3 \times \textcolor{green}{3}] \times [\textcolor{green}{3} \times 1] = \begin{bmatrix} c_{00} & c_{01} & c_{02} \\ c_{10} & c_{11} & c_{12} \\ c_{20} & c_{21} & c_{22} \end{bmatrix} \times \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} x' \\ y' \\ z' \end{bmatrix} $$This approach aligns with the conventions of matrix multiplication, ensuring that vectors or points can be correctly transformed by [3x3] matrices.
Note that the result of this operation is a transformed point written in the form of a [3x1] matrix. This means we start with a point and end with a transformed point, effectively solving our problem. To summarize:
-
Left or Pre-Multiplication: When we choose to represent vectors or points in row-major order ([1x3]), we position the point on the left side of the multiplication, with the [3x3] matrix on the right side. This is represented as:
$$ [1x3] \times [3x3] = [1x3] $$Example:
$$ [x, y, z] \times \textcolor{blue}{ \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}} = [x', y', z'] $$ $$ \begin{array}{rcl} x' & = & x \cdot a_{11} + y \cdot a_{21} + z \cdot a_{31} \\ y' & = & x \cdot a_{12} + y \cdot a_{22} + z \cdot a_{32} \\ z' & = & x \cdot a_{13} + y \cdot a_{23} + z \cdot a_{33} \end{array} $$ -
Right or Post-Multiplication: Conversely, if we opt to express vectors in column-major order ([3x1]), the [3x3] matrix is placed on the left side of the multiplication, with the vector or point on the right side. This is represented as:
$$ [3x3] \times [3x1] = [3x1] $$Example:
$$ \textcolor{red}{ \begin{bmatrix} a_{11} & a_{21} & a_{31} \\ a_{12} & a_{22} & a_{32} \\ a_{13} & a_{23} & a_{33} \end{bmatrix}} \times \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} x' \\ y' \\ z' \end{bmatrix} $$Here is the expanded version of the matrix-vector multiplication:
$$ \begin{array}{rcl} x' & = & a_{11} \cdot x + a_{21} \cdot y + a_{31} \cdot z \\ y' & = & a_{12} \cdot x + a_{22} \cdot y + a_{32} \cdot z \\ z' & = & a_{13} \cdot x + a_{23} \cdot y + a_{33} \cdot z \end{array} $$
You can observe that regardless of whether you present your matrices in a column or row vector format, the result of the matrix-vector multiplication remains the same, which is, of course, what you would expect. The convention used should have no effect on the result.
We will explain later in this chapter why, in the column-vector matrix (the second matrix), the coefficients \(\textcolor{red}{a_{11}}\), \(\textcolor{red}{a_{12}}\), \(\textcolor{red}{a_{13}}\), then \(\textcolor{red}{a_{21}}\), \(\textcolor{red}{a_{22}}\), \(\textcolor{red}{a_{23}}\), and finally \(\textcolor{red}{a_{31}}\), \(\textcolor{red}{a_{32}}\), \(\textcolor{red}{a_{33}}\), are presented in a column fashion rather than being organized as three consecutive rows (as it is the case for the first matrix). This shouldn't really surprise you since we are dealing with "column-vector" organized matrices, but we will revisit this topic next, so don't worry if this still puzzles you.
It's important to use these terms accurately. For example, Maya documentation states, "the matrices are post-multiplied in Maya. To transform a point P from object-space to world-space (P'), you would need to post-multiply by the worldMatrix. (P' = P x WM)", which might seem confusing because it actually describes a pre-multiplication scenario. However, the documentation is referring to the matrix's position relative to the point in this specific context, leading to a misuse of terminology. Correctly, it should state that in Maya, points and vectors are expressed as row-major vectors and are pre-multiplied, indicating the point or vector precedes the matrix in the multiplication order.
The differences between the two conventions can be summarized as follows, where P stands for Point, V for Vector, and M for Matrix.
Row-Major Order
-
Representation: Points or vectors (P/V) are expressed as [1x3] matrices, such as \(P/V = \begin{bmatrix}x & y & z\end{bmatrix}\).
-
Multiplication Convention: Left or pre-multiplication. The point or vector is placed on the left side of the multiplication operation.
-
Operation: \(P/V * M\). The point or vector is multiplied by the matrix, indicating that the transformation matrix follows the vector in the operation.
Column-Major Order
-
Representation: Points or vectors (P/V) are expressed as [3x1] matrices, such as
$$P/V = \begin{bmatrix}x \\ y \\ z\end{bmatrix}$$ -
Multiplication Convention: Right or post-multiplication. The matrix is placed on the left side of the multiplication operation.
-
Operation: \(M * P/V\). The matrix multiplies the point or vector, indicating that the vector or point follows the transformation matrix in the operation.
To summarize (again):
-
In row-major order, vectors or points are typically represented in a single row (as [1x3] matrices), and multiplication by a transformation matrix (M) is done from the right (P/V * M), known as pre-multiplication.
-
In column-major order, vectors or points are represented in a single column (as [3x1] matrices), and the transformation matrix multiplies from the left (M * P/V), referred to as post-multiplication.
As you explore different projects, it's likely you'll encounter various ways in which points and vectors are multiplied. While this may have been confusing before, you now understand why. For example, in a modern graphics API like Vulkan, which relies on the GLSL shading language, the MVP matrix (which stands for model-view-projection matrix—don’t worry if you’re unfamiliar with it for now, it’s just a 4x4 matrix) is used as follows:
gl_Position = MVP * vec4(inPosition, 1.0);
As you can see, in this example, the matrix is on the left side of the point, indicating post-multiplication. This suggests that GLSL, the shading language Vulkan relies on, uses column-major ordering by default (though this can be configured, but that’s a topic for another time). In the other popular shading language used for GPU graphics, HLSL, the default ordering is row-major. Annoying, right?
Difference Between Row-Major and Column-Major Conventions
Understanding the difference between row-major and column-major conventions is not just a matter of notation but also has practical implications in mathematics and computer graphics. Here's an exploration of how these conventions affect matrix multiplication and transformations, and why one might be preferred over the other in certain contexts.
Row-Major vs. Column-Major in Matrix Multiplication
When calculating the product of two matrices, A and B, the process involves multiplying each element of a row in matrix A by the corresponding element of a column in matrix B and summing the results. The approach varies between the row-major and column-major conventions:
-
Row-Major Order: Multiplication is performed as follows:
$$\begin{bmatrix}x & y & z\end{bmatrix} * \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}$$Resulting in:
$${\begin{array}{l}x' = x * a + y * d + z * g\\y' = x * b + y * e + z * h\\z' = x * c + y * f + z * i\end{array}}$$ -
Column-Major Order: The multiplication is:
$$\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} * \begin{bmatrix}x\\y\\z\end{bmatrix}$$Producing:
$${\begin{array}{l}x' = a * x + b * y + c * z\\y' = d * x + e * y + f * z\\z' = g * x + h * y + i * z\end{array} }$$
We use the same matrix and the same point, but the two different approaches yield different results. This is clearly not what we want. When transforming a point using a matrix, we expect the resulting transformed point to be the same regardless of the approach. To achieve this, you can transpose the matrix. For the sake of this example, let's transpose the matrix used in the multiplication where the matrix and vectors are supposed to be organized in columns.
For a refresher on matrix transposition, refer to the chapter on Matrix Operations. As a quick reminder, transposition involves swapping the elements along the diagonal of the matrix, such that, for example, \( m[0][1] \) becomes \( m[1][0] \), \( m[0][2] \) becomes \( m[2][0] \), and so on.
For example:
$$ \begin{bmatrix} a & d & g \\ b & e & h \\ c & f & i \end{bmatrix} * \begin{bmatrix} x \\ y \\ z \end{bmatrix} $$Produces:
$$ \begin{array}{l} x' = a * x + d * y + g * z \\ y' = b * x + e * y + h * z \\ z' = c * x + f * y + i * z \end{array} $$With this transposition applied, you can now see that the resulting transformed point matches the transformed point obtained by multiplying the point in row-major order by the original matrix (without transposition).
Practical Application and Preference
As mentioned before, the choice between row-major and column-major ordering affects how you write transformations, with the point or vector placed either before or after the matrix. For instance:
-
Row-Major Transformations: With row-major matrices and vectors, we would write \( P \times M \). One might argue that writing \( M \times P \) is just as natural as writing \( P \times M \). However, I would counter that we typically think of a point being transformed by a matrix, not the other way around, or we say "let's multiply this point by this matrix"—not the reverse. For this reason, this notation feels more natural to me, as it aligns with how we express this type of operation verbally.
Now, consider chained transformations, where we multiply the point \( P \) by a translation matrix, followed by a rotation around the z-axis, and then a rotation around the y-axis, as in the following example:
$$ P' = P \times T \times R_z \times R_y $$Similarly, I find this way of writing transformations more natural than the alternative, where the matrices are written in reverse order (see below). However, this might just depend on how your brain is wired. For someone else, the column-major transformation order might feel more intuitive. Let me know.
-
Column-Major Transformations: When using column-major vectors and matrices, you will need to write the same sequence of transformations in reverse order, which might seem counter-intuitive (at least to me, and hopefully to most of you):
$$ P' = R_y \times R_z \times T \times P $$
The distinction between row-major and column-major conventions prompts a discussion on preference. Both approaches are legitimate, with mathematics and physics typically favoring column vectors for various reasons, including historical context and the practical explanations provided below. For Scratchapixel, I decided to adopt the row-major order convention, which I also tend to promote in professional work, primarily because it aligns more intuitively with the concept of "this code transforms this point by this matrix." To me, this feels more efficient overall than writing an equation where transformations appear in reverse order, starting with the transformation that is applied last. At least for educational purposes, I think it's a better choice of convention.
When It Comes to Computers: The Cache Locality Myth
Now, note that everything we've written so far about the row- vs. column-major convention only applies to how you write matrices and operations such as point-matrix or matrix-point operations on paper. This is how you should be writing them down, especially if you wish to publish, say, a paper on an algorithm you've designed. However, there's a considerable problem when it comes to implementing these conventions in the world of computers. I'll try to be as clear (and definitive) on this topic as possible, because it’s a rather confusing subject and one of the most debated topics in computer graphics programming.
The source of this confusion stems from OpenGL, which has been—and remains—one of the most popular real-time graphics APIs for decades. Due to its popularity, OpenGL imposed its own design choices on developers (not that we had much choice), but more importantly, it created a trail of legacy habits that, I’d argue, aren’t particularly healthy. Some of the newer, modern real-time graphics APIs, such as Vulkan, have inherited some of these questionable design choices from OpenGL (though this doesn’t make OpenGL any less of a great API). One of these questionable choices is related to matrix ordering.
It turns out that OpenGL is said to use "column-major" matrices. The problem is: what does this really mean? Well, here’s what it means. Let’s take the Perspective Projection Matrix as an example. Some of you may not have studied it yet, but that’s not important for this context, as we don’t need to understand its purpose or how it works right now. It’s just a nice example because, first, it was one of the primary sources of confusion for developers, and second, its coefficients are easily identifiable. So, let's proceed. Here is the matrix as it is presented in the OpenGL documentation:
$$ \begin{pmatrix} \colorbox{yellow}{$\frac{2n}{r-l}$} & \colorbox{cyan}{0} & \colorbox{lightpink}{$\frac{r+l}{r-l}$} & \colorbox{magenta}{0} \\ \colorbox{yellow}{0} & \colorbox{cyan}{$\frac{2n}{t-b}$} & \colorbox{lightpink}{$\frac{t+b}{t-b}$} & \colorbox{magenta}{0} \\ \colorbox{yellow}{0} & \colorbox{cyan}{0} & \colorbox{lightpink}{$-\frac{f+n}{f-n}$} & \colorbox{magenta}{$-\frac{2fn}{f-n}$} \\ \colorbox{yellow}{0} & \colorbox{cyan}{0} & \colorbox{lightpink}{-1} & \colorbox{magenta}{0} \end{pmatrix} $$I have highlighted the columns to emphasize that this is a column-major matrix. Just in case you think I’m imagining things, here’s a picture from the OpenGL Programming Guide appendices, where you can find a reference to the matrix.

The problem arises when readers see a matrix written that way and then try to access m[2][3], expecting to get \(-2fn/(f-n)\). However, that's not what they actually get; they get something else. This discrepancy is precisely what I will explain next. This confusion is a significant source of misunderstanding about column-major vs. row-major matrices in the computer graphics programming community. If OpenGL had decided to use row-major matrices in their specifications, our world might have been a bit simpler.
Now, before we explain what you will get for m[2][3], let's see how you would represent this as a row-major matrix (this is simply the transpose of the above matrix, as you are now aware):
What I want you to focus on now is how the OpenGL column-major matrix is/was stored in the computer's memory.
void glhFrustumf2(float *matrix, float left, float right, float bottom, float top,
float znear, float zfar)
{
float temp, temp2, temp3, temp4;
temp = 2.0 * znear;
temp2 = right - left;
temp3 = top - bottom;
temp4 = zfar - znear;
matrix[0] = temp / temp2;
matrix[1] = 0.0;
matrix[2] = 0.0;
matrix[3] = 0.0;
matrix[4] = 0.0;
matrix[5] = temp / temp3;
matrix[6] = 0.0;
matrix[7] = 0.0;
matrix[8] = (right + left) / temp2;
matrix[9] = (top + bottom) / temp3;
matrix[10] = (-zfar - znear) / temp4;
matrix[11] = -1.0;
matrix[12] = 0.0;
matrix[13] = 0.0;
matrix[14] = (-temp * zfar) / temp4;
matrix[15] = 0.0;
}
If you don't see what's peculiar about this matrix, you need to remember that a matrix in C/C++ can be expressed as follows:
// C++
class Matrix4x4 {
float m[4][4];
};
// C
typedef float vec4[4];
typedef vec4 mat4x4[4];
Perhaps the C version better illustrates that a matrix in your C/C++ program is essentially an array of 4 arrays of 4 floats, or 4 vec4 objects. This means that all these floats are stored contiguously in memory. In essence, you can write:
mat4x4 m;
float* m_ptr = &m[0][0];
for (uint32_t i = 0; i < 16; ++i) {
printf("%d: %f\n", i, *(m_ptr++));
}
It would effectively print out the 16 coefficients of your matrix, scanning the four coefficients pointed to by m[0], then the next four coefficients pointed to by m[1], and so on. What I want you to take away from the code example above is that the 16 coefficients of the matrix are stored contiguously in memory. They occupy a memory block that is 16 times the size of a float (4 bytes), where m[0], or &m[0][0], points to the first coefficient in that block.
Now that we understand this, it's easier to grasp that each "row" of the mat4x4 matrix—m[0], m[1], m[2], and m[3]—actually stores the first, second, third, and fourth columns of the perspective matrix, respectively. Yes, you read that right: each of the four vectors making up the mat4x4 object, which you might think of as rows from a programming perspective (since each vector stores four floats contiguously in memory, and the vectors themselves are contiguous), actually holds the coefficients of the perspective projection matrix's columns. m[0] stores the coefficients of the matrix's first column, m[1] the coefficients of the second column, and so on.
Have a look at the glhFrustumf2 code again, if necessary. The coefficients stored in m[0] are highlighted in yellow, those stored in m[1] are highlighted in cyan, the coefficients stored in m[2] are highlighted in pink, and those in m[3] are highlighted in magenta. As you know, the yellow coefficients come from the matrix's first column, the cyan ones from the second column, and so on.
In other words, m[X], even though from a programming standpoint is a row of 4 floats (4 floats stored contiguously in memory), actually encodes the coefficients of the matrix's columns. So, for instance, m[0] gives you access to the first column of the OpenGL perspective matrix, while m[2] gives you access to the coefficients of the third column, and so on.
Now, let's see how we would perform a point-matrix multiplication with this code. To simplify the process, I'll represent the matrix using letters for the coefficients. I’ll assume that the matrix I start with is a row-major matrix, and I will transpose the coefficients to write the corresponding column-major matrix.
$$ \begin{pmatrix} \colorbox{yellow}{$a$} & \colorbox{yellow}{$b$} & \colorbox{yellow}{$c$} & \colorbox{yellow}{$d$} \\ \colorbox{cyan}{$e$} & \colorbox{cyan}{$f$} & \colorbox{cyan}{$g$} & \colorbox{cyan}{$h$} \\ \colorbox{lightpink}{$i$} & \colorbox{lightpink}{$j$} & \colorbox{lightpink}{$k$} & \colorbox{lightpink}{$l$} \\ \colorbox{magenta}{$m$} & \colorbox{magenta}{$n$} & \colorbox{magenta}{$o$} & \colorbox{magenta}{$p$} \end{pmatrix} \begin{pmatrix} \colorbox{yellow}{$a$} & \colorbox{cyan}{$e$} & \colorbox{lightpink}{$i$} & \colorbox{magenta}{$m$} \\ \colorbox{yellow}{$b$} & \colorbox{cyan}{$f$} & \colorbox{lightpink}{$j$} & \colorbox{magenta}{$n$} \\ \colorbox{yellow}{$c$} & \colorbox{cyan}{$g$} & \colorbox{lightpink}{$k$} & \colorbox{magenta}{$o$} \\ \colorbox{yellow}{$d$} & \colorbox{cyan}{$h$} & \colorbox{lightpink}{$l$} & \colorbox{magenta}{$p$} \end{pmatrix} $$For row-major matrices, storing the coefficients is simpler because each matrix row of coefficients will naturally map to one of the mat4x4's vec4. So, the layout in memory will be as follows:
For column-major matrices, storing the coefficients is similar to how it's done in glFrustum, where we map the coefficients of each matrix column to the corresponding vec4 in the mat4x4 structure.
In other words, as you can see, there is strictly no difference in how row-major and column-major matrices are laid out in a computer's memory. This is important because there's a common misconception floating around on the internet that column-major matrices are better than row-major matrices because, supposedly, during a matrix-point multiplication, the coefficients used in the multiplication are memory-contiguous, which "theoretically" improves cache locality.
The following image is intended to summarize what we've discussed so far in a visual form, hopefully clearing up any remaining doubts.
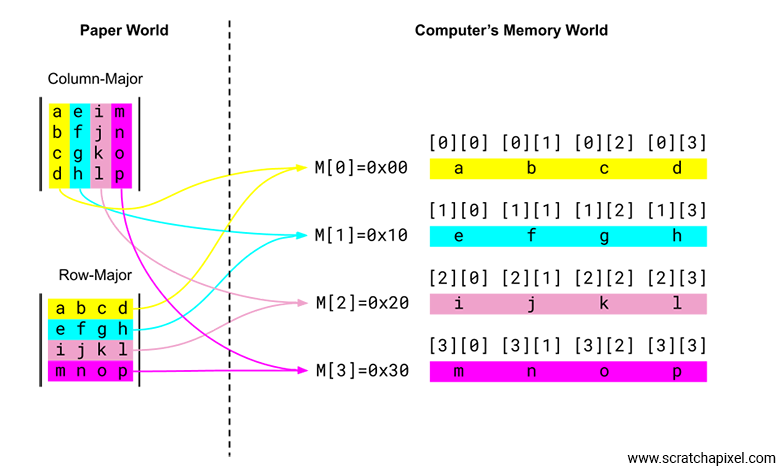
On the right, we've represented the matrix as it exists in your C/C++ program. As you can see, the memory of the 4 vec4 objects is contiguous (the four vec4 objects are stored in a continuous memory block spanning 16 floats). Although we can view each of these 4 vec4 objects as the rows of the matrix in the computer's memory. On the left, we've represented the matrices as they are written on paper, with the column-major matrix at the top and the row-major matrix at the bottom. Notice how each column of the column-major matrix maps to a row in the computer matrix, and how each row of the row-major matrix maps to a row in the computer matrix. The most important thing to note is that the memory layout ends up being exactly the same, regardless of the convention used to write the matrix on paper.
Let's look at what happens when we use these floats in a point-matrix multiplication:
r.x = /*a*/m[0][0]*v.x+/*e*/m[1][0]*v.y+/*i*/m[2][0]*v.z+/*m*/m[3][0]; r.y = /*b*/m[0][1]*v.x+/*f*/m[1][1]*v.y+/*j*/m[2][1]*v.z+/*m*/m[3][1]; r.z = /*c*/m[0][2]*v.x+/*g*/m[1][2]*v.y+/*k*/m[2][2]*v.z+/*n*/m[3][2];
The values m[0][0], m[1][0], m[2][0], and m[3][0] do not follow each other in memory. This is not a cache-friendly layout. To be cache-friendly, the floats used in the calculation of each coordinate of the transformed point should be contiguous in memory, but they are not; they are 4 floats apart from one another (as shown in the image below). Therefore, there is no cache locality here.
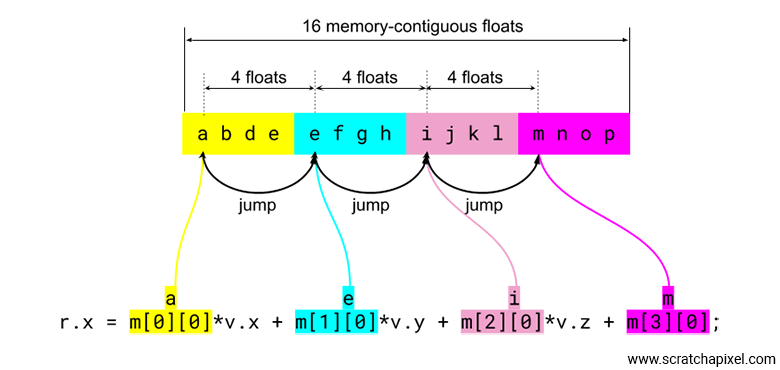
Again, the reason why this point is important is because you will sometimes see people on forums claiming that using column-major ordered matrices is supposedly better for point-matrix multiplication due to improved cache locality, as a result of having the coefficients laid out contiguously in memory. This is not true. To be clear, when it comes to C/C++ and matrices like the OpenGL matrix we showed earlier—written on paper in column-major order but stored in the program's memory in row-major fashion (where the columns of the matrix are stored as the mat4x4's rows, or the vec4s)—there is absolutely no benefit. Period. Anybody who claims otherwise is mistaken.
Moreover, in C/C++, the issue of cache locality vs. non-locality when it comes to 4x4 matrix-point multiplication is just a false problem. We have tested programs with different configurations of how the coefficients of a 4x4 matrix are stored in memory, and we have not observed any significant difference in performance or memory usage in practice. Therefore, people should probably stop debating this non-issue.
However, to avoid sounding too radical, the problem is obviously more subtle than what we've described. Techniques like cache prefetching allow the CPU to predict which memory locations will be needed soon based on current memory access patterns and fetch data into the cache in advance, thereby avoiding delays caused by memory latency.
Typically, prefetching assumes spatial locality, meaning that if a program accesses one memory location, it is likely to access nearby locations soon. This is why, when you access one float, the CPU may fetch a few more contiguous floats from memory into the cache (often in blocks called cache lines, which are usually 64 bytes or 16 floats for modern processors).
Armed with this knowledge, you can see that since the floats used in the computation of one coordinate of the transformed point are not memory-contiguous, the CPU may still prefetch data based on past access patterns. However, it might also fetch unneeded floats into the cache. For example, in a point-matrix multiplication where floats are 4 bytes apart, prefetching could pull in unrelated floats that won't be used, wasting cache bandwidth.
There are ways (using compiler instructions or intrinsics) to instruct the compiler to generate specific prefetch instructions in the machine code it outputs. However, this is an advanced topic left for you to explore on your own. For most recreational programming and even serious development, you may not need to worry about these intricacies, as modern compilers and CPUs are increasingly capable of optimizing and predicting behaviors for you. It's often best not to interfere, unless you're deep into CPU "voodoo."
There's another point that, as a programmer, you need to be careful about, and it's probably far more impactful than this cache locality debate: knowing whether the data you are using is memory-aligned or not. This topic is related to how computers fetch data from RAM, and interested readers can look up terms like "cache lines" on the internet. I’m not going to delve into this here, as it is definitely an advanced topic, but be aware that there are likely more issues in your code due to alignment problems than due to a lack of cache locality in 4x4 matrices, per se.
While these topics are somewhat related, the impact on performance for an object as small as a matrix is minimal, especially considering that there aren’t many matrices in a program's memory and they are small objects compared to larger data structures like mesh points, normals, or index arrays, for which memory alignment is indeed critical. Debating matrix alignment and cache locality is really nitpicking.
The key takeaway from all these explanations is this:
First, if someone tells you they are using column-major matrices in C/C++—like OpenGL matrices, where the columns are stored in the rows of a matrix—to improve cache locality, that explanation is simply untrue. Period.
Second, it doesn’t matter whether your matrices are written on paper in row-major or column-major order. In the computer’s memory (at least in C/C++), they are laid out the same way if you store the columns of the column-major matrices into the rows of the program's matrix. Therefore, your code should work regardless of the convention you use to write matrices on paper.
There's one possible explanation for this "cache-locality" myth though (in addition to what we've said above). It may stem from the fact that some rather unusual programming languages, such as FORTRAN (and also MATLAB), store two-dimensional arrays in memory differently than C/C++. Let's imagine we assign the coefficients of a matrix in C/C++ like this:
v[0][0] = 1; v[0][1] = 2; v[0][2] = 3; v[0][3] = 4; v[1][0] = 5; v[1][1] = 6; v[1][2] = 7; v[1][3] = 8; // ... and so on
In C/C++, the row-major memory layout would look like this:
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]
Now, let's say we're doing a point-matrix multiplication:
r.x = 1 * v.x + 5 * v.y + 9 * v.z + 13; r.y = 2 * v.x + 6 * v.y + 10 * v.z + 14; r.z = 3 * v.x + 7 * v.y + 11 * v.z + 15;
As you know by now, the coefficients 1, 5, 9, 13 used in the first row of the calculation are not contiguous in memory. They are 4 floats apart from one another. So, there is no cache locality here.
Now, let's write the same matrix in FORTRAN:
v(1,1) = 1 v(1,2) = 2 v(1,3) = 3 v(1,4) = 4 v(2,1) = 5 v(2,2) = 6 v(2,3) = 7 v(2,4) = 8 // ... and so on
However, FORTRAN uses a column-major memory layout. That is, FORTRAN would store the coefficients like this:
[1, 5, 9, 13, 2, 6, 10, 14, 3, 7, 11, 15, 4, 8, 12, 16]
In this particular case, when you do a point-matrix multiplication in FORTRAN, you do have cache locality because the point-matrix multiplication internally looks like this:
r.x = 1 * v.x + 5 * v.y + 9 * v.z + 13; r.y = 2 * v.x + 6 * v.y + 10 * v.z + 14; r.z = 3 * v.x + 7 * v.y + 11 * v.z + 15;
And yes, in this particular case, the values 1, 5, 9, 13 are stored contiguously in memory, thanks to the way FORTRAN organizes the coefficients of two-dimensional arrays (for you).
Wrapping Up!
To wrap things up, I don't think there's much left to say, as hopefully, the explanation above has been clear enough to help you understand the difference between row-major and column-major matrices. When it comes to programming, if you decide to store the columns of your supposedly column-major matrix or the rows of your row-major matrix into the rows of your program's matrix (assuming you are using a C/C++ object like an array of vec4 or an array of 4 arrays of 4 floats), the coefficients will end up being packed in memory the same way regardless.
With the possible caveat of cache line prefetching and alignment—which you shouldn't worry too much about unless you really know what you're doing and are working on an application that needs to be super highly optimized—this isn't a major concern, considering how small the matrix object is.
Now, you might wonder why people say that certain graphics APIs like OpenGL, Vulkan, or DirectX use row-major or column-major matrices, and whether this is something you should pay attention to. The answer is both yes and no. First of all, APIs like Vulkan or DirectX don’t really enforce row-major or column-major conventions. In OpenGL, it mattered because this was how matrices were presented in their specifications and documentation, which led people to expect the coefficients to be located in a specific way in memory that matched how they were written on paper.
This problem aside, the reason I mentioned that Vulkan doesn’t care about matrix ordering is because it’s not Vulkan itself that is concerned here, but rather the shading language it uses—in this case, GLSL (the same shading language used by OpenGL). Indeed, when you write a shader—whether it's a vertex or fragment shader in GLSL—you need to follow certain conventions to get the right result in your application:
vec4 r = M * vec4(vertex_pos, 1);
Instead of:
vec4 r = vec4(vertex_pos, 1) * M;
Even though the matrix coefficients in memory are organized as shown earlier, GLSL still expects that you perform the multiplication in the form of post-multiplication (i.e., the vector comes after the matrix). If you write the matrix after the vector, you won't get the correct result. So, as a convention, GLSL expects you to perform point-matrix multiplication using post-multiplication notation, as if the matrix were indeed column-major. Don't ask me why—that's just the rule.
For a long time, there was no way to get around this. If you were using row-major matrices in your thinking, you had to switch your mindset when writing shaders in GLSL and perform the multiplication the opposite way. Thankfully, not too long ago, the people responsible for the language introduced a way to specify that you prefer to use row-major conventions consistently. In GLSL, you can achieve this by writing:
layout(row_major) uniform mat4 myMatrix; // now you can write vec4 r = vec4(vertex_pos, 1) * myMatrix;
This allows you to be consistent across your codebase, whether in C/C++ or GLSL shader code, if you prefer the row-major convention.
Conclusion
Whether you use column-major or row-major matrices will always be a bit of a political or religious debate with no clear winner. That said, for the reasons mentioned earlier—such as the fact that writing P * M aligns better with how we naturally speak about point-matrix multiplication ("I then multiply this point by this matrix")—I highly recommend sticking to the right-hand coordinate system (with Y up) and using row-major matrices. This way, you'll avoid situations where, at 1 a.m., you're struggling to figure out why your matrix isn't giving you the expected result. Using row-major matrices aligns naturally with how things are laid out in memory and will make your life simpler. Isn't that all we want in the end?
Peace!