Ray-Tracing: Rendering a Triangle

Why Are Triangles Useful?

In theory, solving ray and triangle intersections is not overly difficult. However, the complexity of ray-triangle intersection arises from the multitude of different cases that must be accounted for. Writing a routine that handles all these cases while being both robust and fast can be challenging. For this reason, the topic has been extensively researched and debated within the computer graphics community. It is also generally considered one of the most critical routines in a ray-tracer (and I will explain why shortly).

There are quite a few possible approaches to this problem, as seen in various open-source projects that use ray tracing, with a couple being more popular than the others.

Among these, you'll find the so-called Möller-Trumbore method, named after the two authors who published the paper "_Fast Minimum Storage Ray-Triangle Intersection_" in 1997. The method was presented at the time as "the fastest ray/triangle intersection routine for triangles that do not have precomputed plane equations" (since earlier algorithms relied on pre-calculating the triangle's plane, as we will learn in this lesson).

The second most common method is the "_Watertight Ray/Triangle Intersection_" (2013), authored by Sven Woop, Carsten Benthin, and Ingo Wald (who now works at Nvidia and, as far as I know, leads the "Ray-Tracing" group there). I won't be covering the "Watertight Ray/Triangle Intersection" technique in this lesson. I will devote a separate lesson to it later. The technique itself is not overly complicated, especially since it shares some concepts with the Möller-Trumbore method, but for a beginner’s course, it's not necessary to cover an extensive set of techniques.

Before we dive into the topic, note that methods also exist to calculate the intersection of a ray with a quad. Triangles have neat properties, which we will discuss in this lesson, but you need two triangles to represent a quad. So, if you can calculate a ray-quad intersection that's not significantly slower than the ray-triangle method, it would be a great improvement. Recently, especially with advances in hardware-accelerated ray tracing, ray-quad intersections have regained popularity. Again, this will be covered in another/future lesson.

So, the structure of the lesson will be as follows:

• First, we will review why triangles are cool.

• Then, we will explore a few of their mathematical properties, which we will use to solve the ray-triangle problem.

• Next, we will study a simple geometric method to solve this problem.

• After that, we will learn about barycentric coordinates.

• Finally, we will cover the Möller-Trumbore algorithm.

Geometric Primitives

A geometric primitive represents a 3D object in a rendering program. For instance, to represent a sphere, we can define it by the position of its center and its radius, as explained in the previous lesson. Similarly, complex objects can be modeled by more complex geometric primitives such as polygons, NURBS or Bezier patches, subdivision surfaces, etc. Each one is useful for representing certain types of 3D objects. For example, NURBS are suitable for objects with smooth surfaces, while polygons are useful for geometric shapes like buildings. A triangle is not a distinct geometry type but rather a subset of the polygon primitive type. We will learn in a later lesson that a polygonal object is easily convertible into triangles.

Why Do We Like Triangles so Much?

Calculating a ray's intersection with a primitive such as a sphere is straightforward. However, modeling most 3D objects solely with spheres is impractical, which necessitates the use of other types of primitives to represent more complex objects with arbitrary shapes. While there is no restriction on using polygonal meshes or NURBS surfaces in our renderer, computing the intersection of a ray with these primitives can be difficult and time-consuming. Conversely, computing the intersection of a ray with a triangle is a relatively simple process that can be well optimized. It may not be as fast as ray-sphere intersections, but it is more efficient than rendering the intersection of a ray with a NURBS surface. This is a compromise we are willing to accept.

Instead of dealing with complex primitives such as NURBS or Bezier patches, we can convert every object into a triangle mesh and compute the intersection of a ray with each triangle in the mesh. This approach simplifies the ray-object intersection to a single, reasonably fast routine. Converting a Bezier patch into a triangle mesh is much simpler than computing multiple ray-Bezier patch intersections. Alternatively, you might wonder why we don’t just use a ray-sphere intersection method when the geometry is made up of spheres, convert NURBS objects into triangle meshes when we have NURBS objects, and then use a ray-triangle intersection routine. While this is feasible in theory—and I have seen renderers that follow this approach, though quite some time ago—in practice, it is not something we do. This approach significantly complicates the codebase, requiring us to decide which strategy to use for each type of geometry and implement a potentially bespoke ray-geometry intersection routine for each type.

So, as I mentioned, in practice, whenever we implement a new geometric primitive type, rather than writing a special ray-intersection routine for that specific geometry type, we focus our development effort on providing the system with a routine to convert that geometry into a "universal" triangular mesh. The triangle becomes the foundational primitive upon which all our ray-tracing intersection code is built. Most modern ray tracers adopt this strategy (though it used to be slightly different in the old days).

By the way, triangles are not only the foundational primitive of ray tracing but also play a similar role in another rendering method that GPUs still use as their default mode: rasterization. Indeed, every mesh you see rendered in a video game using rasterization is effectively converted into a triangle mesh (with some exceptions for things like lines, points, and other advanced volumetric rendering methods). The reasons why GPUs use triangles as their default rendering primitive in rasterization are quite similar to why we use triangles in ray tracing. Primarily, it's because rendering triangles—whether through rasterization or ray tracing—can be neatly hardware-accelerated by GPUs.

What Is a Triangle?

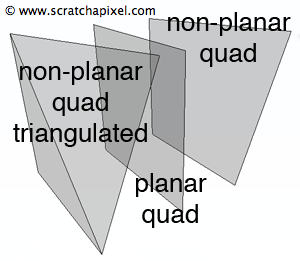
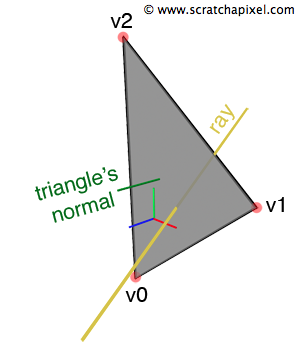
A triangle is defined by three vertices (or points) positioned in three-dimensional space (Figure 1). A single point can represent a location in space. With two points, we can define a line. Three points allow us to define a surface—and specifically, a plane. By construction, a triangle is coplanar; its three vertices delineate a plane, with all three vertices residing within the same plane. This is not necessarily true for polygons with more than three vertices; a quad, defined by four points, may not be coplanar when these points do not reside in the same plane. However, quads can be converted into two coplanar triangles, as illustrated in Figure 2. This technique, known as triangulation, can be applied to polygons with any number of vertices and will be further explored in the context of rendering polygon meshes in the next lesson. For now, we will just focus on rendering a single triangle.

How Do We Compute the Intersection of a Ray With a Triangle?

Over the past few decades, numerous algorithms have been developed to compute the intersection between a ray and a triangle, with ongoing research and new papers regularly being published. As suggested in the introduction, in this lesson, we will introduce two of these techniques. The first technique uses basic logic and elementary linear algebra for implementation, which we will refer to as the *geometric solution* (because it solely relies on geometric principles). The second technique, considered one of the fastest for ray-triangle intersection, was proposed by Möller and Trumbore in 1997 in their paper *"Fast, Minimum Storage Ray-Triangle Intersection."* This method does not rely on the pre-computation of the triangle plane equation, which was required by previous algorithms. While this method requires a more advanced understanding of linear algebra, we will explain it in a clear and comprehensive manner.

We can break down the ray-triangle intersection test into two main steps:

1. Does the ray intersect the plane defined by the triangle?

2. If so, does the intersection point fall within the triangle?

Let's explore how we can address these two questions.